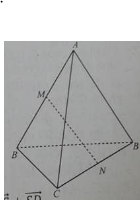
Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{M N}=k(\overrightarrow{A D}+\overrightarrow{B C})\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(\left.\begin{array}{l} \overrightarrow{M N}=\overrightarrow{M A}+\overrightarrow{A D}+\overrightarrow{D N} \\ \overrightarrow{M N}=\overrightarrow{M B}+\overrightarrow{B C}+\overrightarrow{C N} \end{array}\right\} \Rightarrow 2 \overrightarrow{M N}=\overrightarrow{A D}+\overrightarrow{B C}+\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{D N}+\overrightarrow{C N}\)
Mà M và N lần lượt là trung điểm của AB và CD nên \(\overrightarrow{M A}=\overrightarrow{B M}=-\overrightarrow{M B} ; \overrightarrow{D N}=\overrightarrow{N C}=-\overrightarrow{C N}\)
Do đó \(2 \overrightarrow{M N}=\overrightarrow{A D}+\overrightarrow{B C} \Rightarrow \overrightarrow{M N}=\frac{1}{2}(\overrightarrow{A D}+\overrightarrow{B C})\)
.png)











