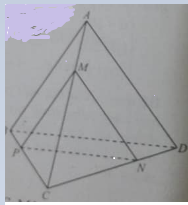
Cho tứ diện ABCD với M, N lần lượt là trọng tâm các tam giác ABD, ACD
Xét các khẳng định sau:
(I) \(MN//mp\left( {ABC} \right)\)
(II) \(MN{\rm{//}}mp\left( {BCD} \right)\)
(III) \(MN{\rm{//}}mp\left( {ACD} \right)\)
(IV)) \(MN{\rm{//}}mp\left( {CDA} \right)\)
Các mệnh đề nào đúng?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai.png)
Gọi I là trung điểm của AD.
Do M, N là trọng tâm tam giác ABD, ACD nên \(\frac{{IM}}{{IB}} = \frac{{IN}}{{IC}} = \frac{1}{3}\)
Theo định lý Talet có MN // BC.
Mà \(BC \subset \left( {BCD} \right),BC \subset \left( {ABC} \right)\).
Vậy \(MN{\rm{//}}\left( {BCD} \right),MN{\rm{//}}\left( {ABC} \right)\).
ADMICRO
YOMEDIA
ZUNIA9