Đồ thị hàm số \(f(x)=\frac{x+1}{\sqrt{x^{2}-1}}\) có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: \(D=(-\infty ;-1) \cup(1 ;+\infty)\)
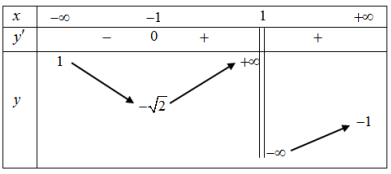
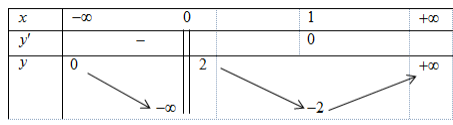
\(+\text { TH1: } x<-1 \Rightarrow x+1<0 .\\ \text { Khi đó } f(x)=\frac{x+1}{\sqrt{x^{2}-1}}=\frac{-\sqrt{(x+1)^{2}}}{\sqrt{(x-1)(x+1)}}=-\sqrt{\frac{x+1}{x-1}}\)
Suy ra hàm số có TCN y = - 1, không có TCĐ.
\(+\text { TH2: } x>1 \Rightarrow x+1>0 .\\ \text { Khi đó } f(x)=\frac{x+1}{\sqrt{x^{2}-1}}=\frac{\sqrt{(x+1)^{2}}}{\sqrt{(x-1)(x+1)}}=\sqrt{\frac{x+1}{x-1}}\)
Suy ra hàm số có TCN y = 1, TCĐ x = 1 .
Vậy hàm số có 2 TCN và 1 TCN
Câu hỏi liên quan
-
Số tiệm cận của hàm số \(y=\frac{\sqrt{x^{2}+1}-x}{\sqrt{x^{2}-9}-4}\) là:
-
\(\text { Cho hàm số } y=f(x) \text { có } \lim _{x \rightarrow-\infty} f(x)=2, \lim _{x \rightarrow+\infty} f(x)=-\infty \text { . }\)Khẳng định nào sau đây đúng?
-
Tìm số tiệm cận đứng của đồ thị hàm số \(y=\frac{x^{2}-3 x-4}{x^{2}-16}\).
-
Đồ thị như hình vẽ là của một trong bốn hàm số được cho ở các phương án A, B, C, D. Hỏi đó là hàm số nào?
-
Cho hàm số \(y = \frac{{3x + 1}}{{2x - 1}}\). Khẳng định nào sau đây đúng?
-
Số đường tiệm cận của đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{x^{3}-x^{2}-x+1}\) là?
-
Đồ thị hàm số \(y=\frac{2 x-1}{x+2}\) có bao nhiêu đường tiệm cận
-
Cho hàm số f(x) xác định, liên tục trên \(\mathbb{R} \backslash\{-1\}\) và có bảng biến thiên như sau:
Khẳng định nào sau đây là sai?
-
Đồ thị của hàm số \(y = \frac{{x + 1}}{{{x^2} + 2x - 3}}\) có bao nhiêu tiệm cận ?
-
Số đường tiệm cận của đồ thị hàm số \(y=\frac{x+3}{\sqrt{x^{2}+1}}\) là:
-
Đồ thị hàm số \(y = \dfrac{{3x + \sqrt {{x^2} + 1} }}{{2 + \sqrt {3{x^2} + 2} }}\) có bao nhiêu đường tiệm cận ngang?
-
Số đường tiệm cận của đồ thị hàm số \(y=\frac{x}{x^{2}-1}\)nằm bên phải trục tung là
-
Đồ thị hàm số \(y=\frac{\sqrt{4-x^{2}}}{x^{2}-3 x-4}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang ?
-
Đồ thị hàm số nào sau đây có nhiều đường tiệm cận nhất?
-
Đồ thị hàm số \(y=\frac{2 x-7}{x+2}\) có bao nhiêu đường tiệm cận?
-
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên sau?
.PNG)
-
Đường thẳng nào sau đây lần lượt là đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 1}}{{x + 2}}\)
-
Cho hàm số có bảng biến thiên như hình sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y=f(x) là -
Cho hàm số \(y=f(x)\) có bảng biến thiên sauKhẳng định nào sau đây đúng
-
Đường tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x-2} 1 \) là:
