Gọi (H) là tập hợp các điểm biểu diễn số phức z thỏa \(1 \leq|z-1| \leq 2\) trong mặt phẳng phức. Tính diện tích hình (H).
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai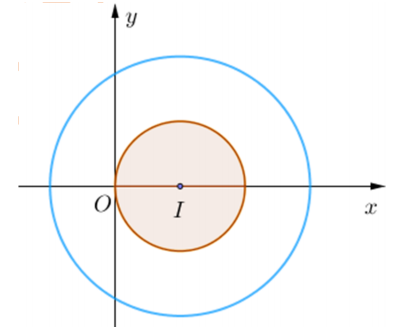
Đặt \(z=x+y i,|z-1|=|x-1+y i|=\sqrt{(x-1)^{2}+y^{2}}\)
Do đó \(1 \leq|z-1| \leq 2 \Leftrightarrow 1 \leq \sqrt{(x-1)^{2}+y^{2}} \leq 2 \Leftrightarrow 1 \leq(x-1)^{2}+y^{2} \leq 4\)
Tập hợp các điểm biểu diễn số phức z là hình phẳng nằm trong đường tròn tâm I(1 ; 0) bán kính R=2 và nằm ngoài đường tròn I(1 ; 0) bán kính r =1. Diện tích hình phẳng \(S=\pi \cdot 2^{2}-\pi \cdot 1^{2}=3 \pi\)
ADMICRO
YOMEDIA
ZUNIA9











