Gọi z1 , z2 là các nghiệm phức của phương trình \(z^{2}-4 z+13=0, \) với z1 có phần ảo dương. Biết số phức z thỏa mãn \(2\left|z-z_{1}\right| \leq\left|z-z_{2}\right|\) , phần thực nhỏ nhất của z là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{aligned} &\text { Ta có } z^{2}-4 z+13=0 \Leftrightarrow z_{1}=2+3 \mathrm{i} \text { hoặc } z_{2}=2-3 \mathrm{i} \text { . }\\ &\text { Gọi } z=x+y \mathrm{i}, \text { với } x, y \in \mathbb{R}\\ &\text { Theo giả thiết, } 2\left|z-z_{1}\right| \leq\left|z-z_{2}\right| \Leftrightarrow 2 \sqrt{(x-2)^{2}+(y-3)^{2}} \leq \sqrt{(x-2)^{2}+(y+3)^{2}}\\ &\Leftrightarrow 4\left[(x-2)^{2}+(y-3)^{2}\right] \leq(x-2)^{2}+(y+3)^{2} \Leftrightarrow(x-2)^{2}+(y-5)^{2} \leq 16 \end{aligned}\)
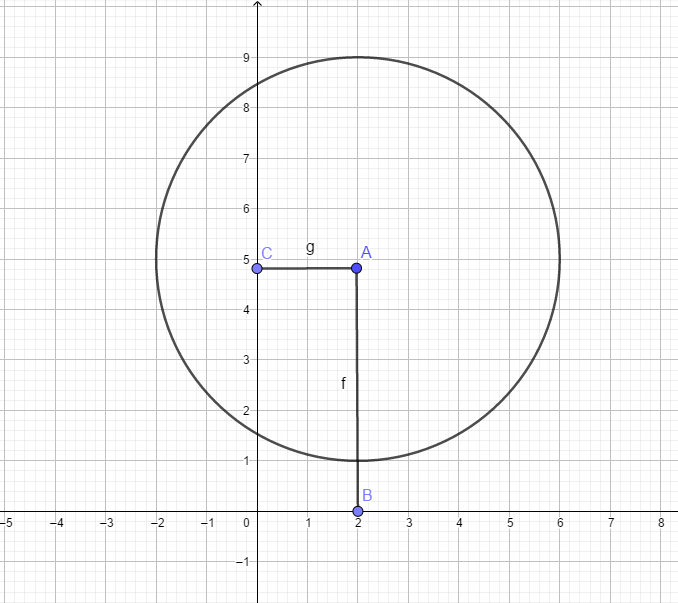
Suy ra tập hợp các điểm biểu diễn số phức z là miền trong của hình tròn (C) có tâm I(2;5) , bán kính R = 4 , kể cả hình tròn đó.
Do đó, phần thực nhỏ nhất của z là \(x_{\min }=-2\)