Xét các số phức \(z, w \text { thỏa }|z-3 \sqrt{2}|=\sqrt{2} \text { và }|w-4 \sqrt{2} i|=2 \sqrt{2} \text { . Biết }|z-w|\) đạt giá trị nhỏ nhất khi
\(z=z_{0} \text { và } w=w_{0}.\) Giá trị của \(\left|3 z_{0}-w_{0}\right|\) bằng:

A. \(2 \sqrt{2}\)

B. \(6 \sqrt{2}\)

C. \(4 \sqrt{2}\)

D. \(8 \sqrt{2}\)

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Toán Lớp 12

Chủ đề: Số phức

Bài: Phương trình bậc hai với hệ số thực

Lời giải:

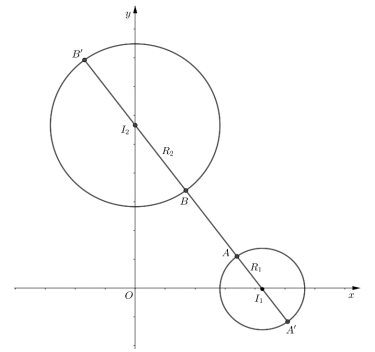
Báo sai

Gọi A ,B là hai điểm biểu diễn cho hai số phức z, w.

+\(|z-3 \sqrt{2}|=\sqrt{2} \Rightarrow A \text { thuộc đường tròn tâm } I_{1}(3 \sqrt{2} ; 0), \text { bán kính } R_{1}=\sqrt{2} \text { . }\)

+\(|w-4 \sqrt{2} i|=2 \sqrt{2} \Rightarrow B \text { thuộc đường tròn tâm } I_{2}(0 ; 4 \sqrt{2}) \text { , bán kính } R_{2}=2 \sqrt{2} \text { . }\)

\(\begin{aligned} &\text { Ta có: } I_{1} I_{2}=\sqrt{9 \times 2+16 \times 2}=5 \sqrt{2} \text { . }\\ &\Rightarrow P=|z-\mathrm{w}|=A B \Rightarrow\left\{\begin{array}{l} P_{\min }=\left|I_{1} I_{2}-R_{1}-R_{2}\right|=2 \sqrt{2} \\ P_{\max }=I_{1} I_{2}+R_{1}+R_{2}=8 \sqrt{2} \end{array}\right.\\ &\overrightarrow{I_{1} I_{2}}=(-3 \sqrt{2} ; 4 \sqrt{2}), \text { phương trình đường thẳng } I_{1} I_{2}: 4 x+3 y-12 \sqrt{2}=0\\ &\left\{\begin{array}{l} 4 x+3 y-12 \sqrt{2}=0 \\ (x-3 \sqrt{2})^{2}+y^{2}=2 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=\frac{12 \sqrt{2}-4 x}{3} \\ \frac{25}{9} x^{2}-\frac{50 \sqrt{2}}{3} x+48=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=\frac{18 \sqrt{2}}{5} \Rightarrow y=\frac{-4 \sqrt{2}}{5} \\ x=\frac{12 \sqrt{2}}{5} \Rightarrow y=\frac{4 \sqrt{2}}{5} \end{array}\right.\right.\right. \end{aligned}\)

Điểm A là điểm nằm bên trong \(I_{1} I_{2}\) nên có toạ độ là \(\left(\frac{12 \sqrt{2}}{5} ; \frac{4 \sqrt{2}}{5}\right)\)

\(\begin{aligned} &\left\{\begin{array}{l} 4 x+3 y-12 \sqrt{2}=0 \\ x^{2}+(y-4 \sqrt{2})^{2}=8 \end{array} \Leftrightarrow\left[\begin{array}{l} y=\frac{28 \sqrt{2}}{5} \Rightarrow x=\frac{-6 \sqrt{2}}{5} \\ y=\frac{12 \sqrt{2}}{5} \Rightarrow x=\frac{6 \sqrt{2}}{5} \end{array}\right.\right.\\ &\text { Điểm } B \text { là điểm nằm bên trong } I_{1} I_{2} \text { nên có toạ độ là: }\left(\frac{6 \sqrt{2}}{5} ; \frac{12 \sqrt{2}}{5}\right) \text { . }\\ &\text { Theo đó } A, B \text { lần lượt biểu diễn cho } z_{0}, w_{0} . \text { Suy ra } z_{0}=\frac{12 \sqrt{2}}{5}+\frac{4 \sqrt{2}}{5} i, \mathrm{w}_{0}=\frac{12 \sqrt{2}}{5}+\frac{4 \sqrt{2}}{5} i \text { . }\\ &\text { Vậy: }\left|3 z_{0}-w_{0}\right|=6 \sqrt{2} \text { . } \end{aligned}\)