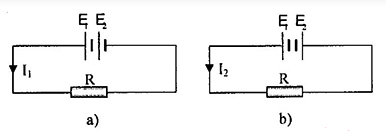
Hai dây đẫn thẳng dài vô hạn, đặt song song trong không khí cách nhau một đoạn d=12cm có các dòng điện cùng chiều I1=I2=I=10A chạy qua. Một điểm M cách đều mỗi dây dẫn một đoạn x. x bằng bao nhiêu để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGiả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi vào tại B. Các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) có phương chiều như hình vẽ:
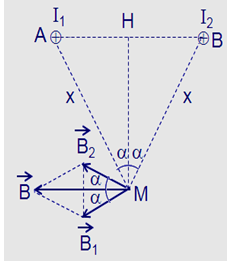
Có độ lớn: \({B_1} = {B_2} = {2.10^{ - 7}}\frac{I}{x}\)
Cảm ứng từ tổng hợp tại M là: \(\vec B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \) có phương chiều như hình vẽ và có độ lớn:
\(B = {B_1}cosa + {B_2}cosa = 2{B_1}cosa = 2{B_1}\frac{{HM}}{{AM}} = {2.2.10^{ - 7}}\frac{I}{x}\frac{{\sqrt {{x^2} - {{\left( {\frac{d}{2}} \right)}^2}} }}{x} = {4.10^{ - 7}}I\sqrt {\frac{1}{{{x^2}}} - \frac{{{d^2}}}{{4{x^4}}}} \)
Nhận thấy, B đạt cực đại khi \(\frac{1}{{{x^2}}} - \frac{{{d^2}}}{{4{x^4}}}\) đạt cực đại
Ta có: \(\frac{1}{{{x^2}}} - \frac{{{d^2}}}{{4{x^4}}} = \frac{4}{{{d^2}}}\frac{{{d^2}}}{{4{x^2}}}\left( {1 - \frac{{{d^2}}}{{4{x^2}}}} \right)\)
Do \(d < x \to 1 - \frac{{{d^2}}}{{4{x^2}}} > 0\)
Áp dụng BĐT cosi ta có:
\(\frac{{{d^2}}}{{4{{\rm{x}}^2}}}(1 - \frac{{{d^2}}}{{4{{\rm{x}}^2}}}) \le \frac{{{{\left( {\frac{{{d^2}}}{{4{{\rm{x}}^2}}} + 1 - \frac{{{d^2}}}{{4{{\rm{x}}^2}}}} \right)}^2}}}{4} = \frac{1}{4}\)
Câu hỏi liên quan
-
Cho hệ thống như hình vẽ:
.png)
Thanh MN có chiều dài 20cm chuyển động với vận tốc 2m/s2 trong từ trường đều B=0,04T. Tụ điện có điện dung C=2μF. Độ lớn điện tích của tụ điện:
-
Cho mạch điện có sơ đồ như hình vẽ, trong đó : \(E_1 = 8V; r_1 = 1,2Ω; E_2 = 4 V; r_2 = 0,4Ω, R = 28,4Ω;\) hiệu điện thế giữa hai đầu đoạn mạch đo được là UAB = 6V. Cho biết mạch điện này chứa nguồn điện nào và chứa máy thu nào?
-
Một nguồn điện với suất điện động E, điện trở trong r, mắc với một điện trở ngoài R = r thì cường độ dòng điện chạy trong mạch là I. Nếu thay nguồn điện đó bằng 3 nguồn điện giống hệt nó mắc song song thì cường độ dòng điện trong mạch
-
Khi mắc song song n dãy, mỗi dãy có m nguồn, mỗi nguồn có suất đện động E và điện trở trong r giống nhau thì suất điện động và điện trở của bộ nguồn cho bởi biểu thức:
-
Cho mạch điện có sơ đồ như hình vẽ, trong đó : \(E_1 = 8V; r_1 = 1,2Ω; E_2 = 4 V; r_2 = 0,4Ω, R = 28,4Ω\); hiệu điện thế giữa hai đầu đoạn mạch đo được là UAB = 6V. Tính cường độ dòng điện chạy qua đoạn mạch và cho biết chiều của nó.
.PNG)
-
Một bộ nguồn có ba nguồn giống nhau mắc nối tiếp. Mạch ngoài là một điện trở không đổi. Nếu đảo hai cực của một nguồn thì
-
Cho mạch điện có sơ đồ như hình vẽ: \(ξ = 6V, r = 1 \Omega, R_1 = 0,8 \Omega, R_2 = 2 \Omega, R_3 = 3 \Omega\). Cường độ dòng điện chạy qua mạch chính là?
-
Cho mạch điện như hình vẽ. Biểu thức nào sau đây đúng:
-
Mắc bộ nguồn từ a nguồn giống nhau và điện trở của bộ nguồn bằng điện trở của một nguồn thì số a phải là số:
-
Cho mạch điện như hình vẽ: Biết \(E = 30V , r = 1\Omega , R_1 = 12\Omega ,R_2 = 36\Omega, R_3 = 18\Omega ,R_A= 0 \). Tìm số chỉ của ampe kế.
-
Việc ghép nối tiếp các nguồn điện để được bộ nguồn có
-
Chọn đáp án đúng. Việc ghép song song các nguồn điện giống nhau thì
-
Cho đoạn mạch gồm R1 mắc nối tiếp với R2, biểu thức nào sau đây là sai?
-
Bộ nguồn song song là bộ nguồn gồm các nguồn điện
-
Khi mắc n nguồn nối tiếp, mỗi nguồn có suất đện động E và điện trở trong r giống nhau thì suất điện động và điện trở của bộ nguồn cho bởi biểu thức:
-
Một mạch điện kín gồm nguồn điện suất điện động E= 6 v, điện trở trong r=1 nối với mạch ngoài là biến trở R , điều chỉnh R đạt để công sức tiêu thụ trên R đạt giá trị cực đại.Công suất đó là
-
Muốn mắc ba pin giống nhau, mỗi pin có suất điện động 3V thành bộ nguồn 6V thì:
-
Có 3 điện trở \(R_1, R_2, R_3\). Nếu mắc nối tiếp 3 điện trở, rồi mắc vào hiệu điện thế U = 9 V thì dòng điện trong mạch là 1 A; nếu mắc song song 3 điện trở, rồi mắc vào hiệu điện thế U = 9 V thì dòng điện trong mạch chính là 9 A; nếu mắc \((R_1//R_2) nt R_3\), rồi mắc vào hiệu điện thế U = 9 V thì dòng điện trong mạch chính là
-
Cho mạch điện như sau: Biết \(R_1 = R_2 = r \). Cường độ dòng điện chạy trong mạch là:
-
Cho 2 mạch điện như hình vẽ: \(E_1 = 18V,r_1 = 1\Omega. \) Cho \(R = 9 \Omega, I_1 = 2,5A , I_2 = 0,5A \). Tìm E2 và r2
