Một con lắc đơn có chiều dài 81 cm đang dao động điều hòa với biên độ góc 80 tại nơi có g = 9,87m/s2 \((\pi ^2 \approx 9,87) \) Chọn t = 0 khi vật nhỏ của con lắc ở vị trí biên. Quãng đường vật nhỏ đi được trong khoảng thời gian từ t = 0 đến t = 1,2 s là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Chu kì dao động của con lắc đơn:
\( T = 2\pi \sqrt {\frac{l}{g}} = 2\pi \sqrt {\frac{{0,81}}{{9,87}}} = 1,8s\)
\( {\rm{\Delta }}t = 1,2s = \frac{{2T}}{3} = \frac{T}{2} + \frac{T}{6}\)
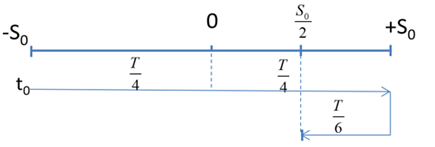
Vẽ trên trục ta được:
⇒ Quãng đường vật đi được trong khoảng thời gian từ t=0 đến t=1,2s là:
\( S = 2{S_0} + \frac{{{S_0}}}{2} = \frac{{5{S_0}}}{2}\)
Lại có: \( {S_0} = l{\alpha _0} = 0,81.\frac{{8\pi }}{{180}}\)
Ta suy ra: \( S=0,28274m=28,3cm\)
Đáp án cần chọn là: D