Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể chèo trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B. Biết anh ấy có thể chèo thuyền 6 km/h , chạy 8 km/h và quãng đường BC = 8(km) . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai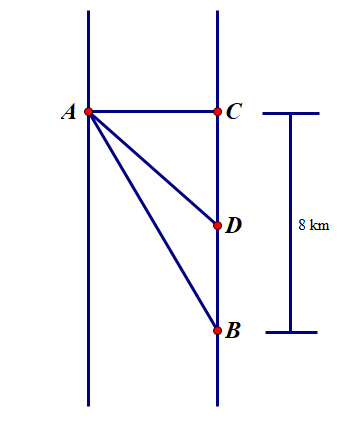
Đặt CD=x . Quãng đường chạy bộ DB=8-x và quãng đường chèo thuyền \(A D=\sqrt{9+x^{2}}\) . Khi đó, thời gian chèo thuyền là \(\frac{\sqrt{9+x^{2}}}{6}\) và thời gian chạy bộ là \(\frac{8-x}{8}\) Tổng thời gian mà người đàn ông cần có là:
\(\begin{array}{l} T(x)=\frac{\sqrt{x^{2}+9}}{6}+\frac{8-x}{8}, \forall x \in[0 ; 8] \\ \text { Ta có: } T^{\prime}(x)=\frac{x}{6 \sqrt{x^{2}+9}}-\frac{1}{8} \\ \begin{array}{l} T^{\prime}(x)=0 \Leftrightarrow \frac{x}{6 \sqrt{x^{2}+9}}=\frac{1}{8} \Leftrightarrow 4 x=3 \sqrt{x^{2}+9} \Leftrightarrow 16 x^{2}=9\left(x^{2}+9\right) \Leftrightarrow 7 x^{2}=81 \Rightarrow x=\frac{9}{\sqrt{7}} \\ \text { Ta có: } T(0)=\frac{3}{2} ; T\left(\frac{9}{\sqrt{7}}\right)=1+\frac{\sqrt{7}}{8} ; T(8)=\frac{\sqrt{73}}{6} \end{array} \\ \text { Do đó: } \min _{[0 ; 8]} T(x)=T\left(\frac{9}{\sqrt{7}}\right)=1+\frac{\sqrt{7}}{8} \end{array}\)
Vậy thời gian ngắn nhất mà người đàn ông cần dùng là \(1+\frac{\sqrt{7}}{8} \approx 1,33(h)\) bằng cách chèo thuyền đến điểm D cách C một khoảng \(\frac{9}{\sqrt{7}}(k m)\) rồi từ đó chạy bộ đến điểm B