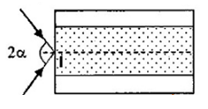
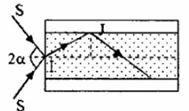
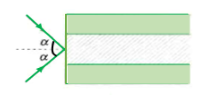
Một ống dẫn sáng hình trụ với lõi có chiết suất n1 = 1,6 và phần vỏ bọc ngoài có chiết suất \(n_2= \sqrt2\). Chùm tia tới hội tụ tại mặt trước của ống tại điểm I với góc \(2\alpha\). Xác định \(\alpha\) nhỏ nhất để tia sáng trong chùm đều truyền được trong ống.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTại I, ta có: \(1.sinα=1,6sinr (1)\)
Để tia sáng truyền đi trong ống thì tại J phải xảy ra hiện tượng phản xạ toàn phần
Ta có: góc tới tại J là: \(i_2=90^0−r\)
Góc giới hạn tại J là: \( \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{\sqrt 2 }}{{1,6}} \to {i_{gh}} = {62,11^0}\)
Điều kiện để xảy ra phản xạ toàn phần: \(i_J≥i_{gh}↔90^0−r≥62,11^0→r≤27,89^0\)
ta có, \(α_{min}⇔r=27,89^0\) thay vào (1), ta được:
\(sinα_{min}=1,6sinr=1,6.sin27,89^0≈0,75→α_{min}=48,6^0\)