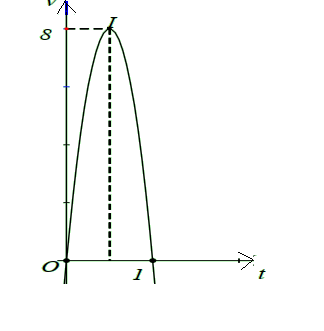
Một vật bắt đầu chuyển động \(v(t)=2 t^{3}-15 t^{2}+24 t+20(\mathrm{~m} / \mathrm{s})\) . Hỏi trong 5 giây đầu tiên, quãng đường vật đi được cho đến khi đạt vận tốc lớn nhất là bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l} \text { Xét hàm số } f(t)=2 t^{3}-15 t^{2}+24 t+20 \text { trên đoạn }[0 ; 5]\\ f^{\prime}(t)=6 t^{2}-30 t+24 ; f^{\prime}(t)=0 \Leftrightarrow\left[\begin{array}{l} t=1 \\ t=4 \end{array}\right.\\ f(0)=20 ; f(1)=31 ; f(4)=4 ; f(5)=15\\ \text { Do đó } \max\limits _{[0 ; 5]} f(t)=f(1)=31 \end{array}\)
Quãng đường đi được từ lúc vật tăng tốc đến khi đạt vận tốc lớn nhất là:
\(S=\int_{0}^{1}\left(2 t^{3}-15 t^{2}+24 t+20\right) \mathrm{d} t=\left.\left(\frac{1}{2} t^{4}-5 t^{3}+12 t^{2}+20 t\right)\right|_{0} ^{1}=\frac{55}{2} \mathrm{~m} .\)
Câu hỏi liên quan
-
Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x \)
-
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-2 x+1, y=x+1, x=0, x=m,(0<m<3)\) bằng:
-
Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned} &(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và } \text { (d): } y=4 \end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằng -
Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle y = 2 - {x^2},y = 1\), quanh trục \(\displaystyle Ox\).
-
Cho hàm số y=f( x ) liên tục trên đoạn [ a;b ]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f( x ), trục hoành và hai đường thẳng x=a,x=b ( a<b ). Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
-
Cho hình H giới hạn bởi đường cong y2 + x = 0, trục Oy và hai đường thẳng y = 0,y = 1. Thể tích khối tròn xoay tạo thành khi quay H quanh trục Oy )được tính bởi:
-
Cho hàm số \(y=(x-2)^{2}\) có đồ thị (C) , khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi (C) , trục Ox , trục Oy và đường thẳng x = 3 có thể tích là -
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)
-
Thể tích khối tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi các đồ thị hàm số \(y=2 x-x^{2}, y=x\) , quanh trục Ox là
-
Diện tích của hình phẳng được giới hạn bởi các đường \(\displaystyle y = \tan x,y = 0,x = - \frac{\pi }{4}\) và \(\displaystyle x = \frac{\pi }{4}\) bằng
-
Tính diện tích hình phẳng giới hạn bởi các đường có phương trình \(x = {y^3}\), \(y = 1\), và \(x = 8\).
-
Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay
có thể tích là
-
Một vật chuyển động với vận tốc đấu là v( ) 0 ( ) m s / và có gia tốc được cho bởi công thức \(a(t)=v^{\prime}(t)=\frac{2}{t+1}\left(m / s^{2}\right)\). Vận tốc của vật sau 15 giây là \(v(15)=8 \ln 2-\log 100(m / s)\) . Tính vận tốc ban đầu của vật.
-
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục \(\displaystyle Ox\) hình phẳng giới hạn bởi các đường \(\displaystyle y = \frac{1}{x}\), \(\displaystyle y = 0,x = 1\) và \(\displaystyle x = a\left( {a > 1} \right)\).
-
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t ,(h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát
-
Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = 0\) và \(x = \pi \), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\;(0 \le x \le \pi )\) là một tam giác đều cạnh \(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} \).
-
Giả sử một vật từ trạng thái nghỉ t=0(s) chuyển động thẳng với vận tốc \(v_{t}=t(5-t)(\mathrm{m} / \mathrm{s})\) . Tính quãng đường vật đi được cho tới khi nó dừng lại.
-
Cho hình (H) giới hạn bởi đường cong \(x = \sqrt y \), trục tung và hai đường thẳng y = 1,y = 4 Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính theo công thức
-
Diện tích hình phẳng giới hạn bởi các đường \(y = x^2 - x , y = 2x - 2 , x = 0 , x = 3\) được tính bởi công thức:
-
Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle y = {x^3} - 1\) và tiếp tuyến với \(\displaystyle y = {x^3} - 1\) tại điểm \(\displaystyle \left( { - 1; - 2} \right)\).
