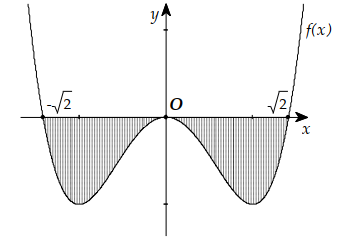
Cho hình phẳng H giới hạn bởi \(y= {\frac{1}{3}{x^3} - {x^2}}\) và Ox. Thể tích khối tròn xoay sinh ra khi quay H quanh Ox bằng :
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(\frac{1}{3}{x^3} - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 3 \end{array} \right.\)
\(\begin{array}{l} V = \pi \mathop \smallint \limits_0^3 {\left( {\frac{1}{3}{x^3} - {x^2}} \right)^2}d{\rm{x\;}} = \pi \mathop \smallint \limits_0^3 \left( {\frac{1}{9}{x^6} - \frac{2}{3}{x^5} + {x^4}} \right)dx\\ = \pi (\frac{1}{{63}}{x^7} - \frac{1}{9}{x^6} + \frac{1}{5}{x^5}) = \frac{{81}}{{35}}\pi \end{array}\)
Câu hỏi liên quan
-
Cho hình phẳng D giới hạn bởi đường cong y= ex, trục hoành và các đường thẳng (x=0,x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
-
Cho hàm số y=f( x ) liên tục trên đoạn [ a;b ]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f( x ), trục hoành và hai đường thẳng x=a,x=b ( a<b ). Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
-
Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10, (ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Có bao nhiêu trẻ được sinh trong khoảng thời gian này (tức là trong 10 năm đầu tiên sau chiến tranh)?
-
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x), y=g(x)\) và hai đường thẳng \(x=a, x=b\) , như hình vẽ bên. Khẳng định nào sau đây đúng?
-
Cho hình (H) giới hạn bởi đồ thị hàm số y = x3, trục hoành và hai đường thẳng x = 0,x = 1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:
-
Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle y = {x^3} - 1\) và tiếp tuyến với \(\displaystyle y = {x^3} - 1\) tại điểm \(\displaystyle \left( { - 1; - 2} \right)\).
-
Nam và Hùng tập sút phạt, ai sút trúng gôn nhiều hơn là người thẳng cuộc. Nếu để bóng ở vị trí A thì xác suất trúng vào gôn của Nam là 0,9 còn của Hùng là 0,7. Nếu để bóng ở vị trí B thì xác suất trúng vào gôn của Nam là 0,7 còn của Hùng là 0,8. Nam và Hùng đều đá một quả ở vị trí A và một quả ở vị trí B. Xác suất để Nam thắng cuộc là:
-
Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle y = 2x - {x^2},y = x\), quanh trục \(\displaystyle Ox\).
-
Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = {x^2} + 1\) và \(y = 3 – x\).
-
Tại một noiw không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t)=10 t-t^{2}\), trong đó t ( phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì bắt đầu tiếp đất vận tốc v của khí cầu là?
-
Quay hình phẳng Q giới hạn bởi các đường \( {y_2} = \frac{{2x}}{\pi };{y_1} = \sin x\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng
-
Tính diện tích hình phẳng giới hạn bởi các đường có phương trình \(x = {y^3}\), \(y = 1\), và \(x = 8\).
-
Diện tích (S ) của hình phẳng giới hạn bởi các đường \(y = - x^2 + 2x, ,y = - 3,x = 1 ,x = 2 \) được tính bởi công thức nào dưới đây?
-
Cho đồ thị biểu thị vận tốc của hai xe A và B khởi hành cùng một lúc, bên cạnh nhau và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường Parabol, đồ thị biểu diễn vận tốc của xe B là một đường thẳng ở hình bên. Hỏi sau khi đi được 3 giây, khoảng cách giữa hai xe là bao nhiêu mét?
.PNG)
-
Cho hình phẳng H giới hạn bởi các đường y=f(x),y=0, x=b và x=a (trong đó hàm số f(x) liên tục trên đoạn [b;a]). Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:
-
Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle x + y = 1;x + y = - 1;\) \(\displaystyle x - y = 1;x - y = - 1\)
-
Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=\sqrt{x+1}\) và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:
-
Diện tích S của hình phẳng giới hạn bởi các đường y = 2x, x = - 3, x = - 2. và trục hoành được tính bằng công thức nào dưới đây?
-
Tính diện tích hình phẳng giới hạn bởi các đường \(y=e^{x} ; y=e^{-x} ; x=1\)
-
Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v(t)=t^{2}+10 t(m / s),\) với t là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 (m/s) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
