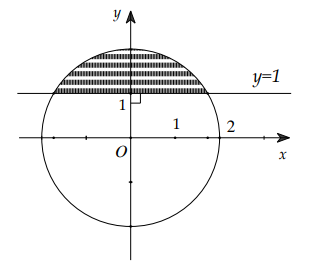
Quay hình phẳng ( H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình đường tròn:
\(x^{2}+(y-1)^{2}=1 \Leftrightarrow(y-1)^{2}=1-x^{2} \Leftrightarrow\left[\begin{array}{l} y=1+\sqrt{1-x^{2}} \\ y=1-\sqrt{1-x^{2}} \end{array}\right.\)
Khi đó \(V=2 \pi \int_{0}^{1}\left[\left(1+\sqrt{1-x^{2}}\right)^{2}-\left(1-\sqrt{1-x^{2}}\right)^{2}\right] \mathrm{d} x=8 \pi \int_{0}^{1} \sqrt{1-x^{2}} \mathrm{~d} x\)
Đặt \(x=\sin t ;\left(t \in\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\right)\)
\(\Rightarrow V=8 \pi \int_{0}^{\frac{\pi}{2}} \cos ^{2} t \mathrm{~d} t=4 \pi \int_{0}^{\frac{\pi}{2}}(1+\cos 2 t) \mathrm{d} t=\left.4 \pi\left(t+\frac{\sin 2 t}{2}\right)\right|_{0} ^{\frac{\pi}{2}}=2 \pi^{2}\)

.PNG)