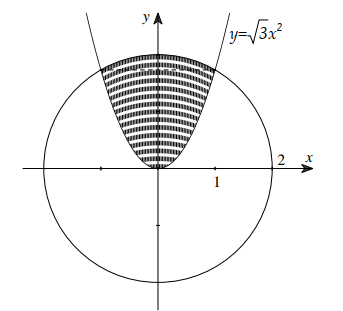
Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐường tròn có phương trình \(x^{2}+y^{2}=4\)
Xét hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}} {{x^2} + {y^2} = 4}\\ {y = \sqrt 3 x} \end{array} \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 1 \end{array} \right.} \right.\)
Do (H) đối xứng nhau qua Oy nên
\(\begin{array}{l} V=2 \pi \int_{0}^{\sqrt{3}}\left[\left(4-x^{2}\right)-(\sqrt{3} x)^{2}\right] \mathrm{d} x=2 \pi \int_{0}^{\sqrt{3}}\left(4-x^{2}-3 x^{4}\right) \mathrm{d} x \\ =\left.2 \pi\left(4 x-\frac{x^{3}}{3}-\frac{3 x^{5}}{5}\right)\right|_{0} ^{\sqrt{3}}=\frac{46 \pi}{15} \end{array}\)
ADMICRO
YOMEDIA
ZUNIA9

.PNG)











