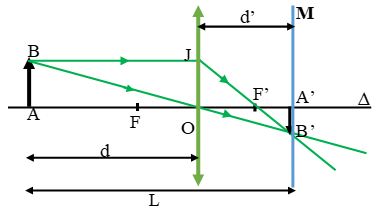
Thấu kính hội tụ có tiêu cự f. Khoảng cách ngắn nhất giữa vật thật và ảnh thật qua thấu kính là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiKhoảng cách giữa vật thật và ảnh thật qua thấu kính hội tụ là
\(\text{L}=\left| \text{d}+\text{d }\!\!'\!\!\text{ } \right|=\text{d}+\text{d }\!\!'\!\!\text{ }=\text{d}+\frac{\text{d}\text{.f}}{\text{d}-\text{f}}=\frac{{{\text{d}}^{2}}}{\text{d}-\text{f}}=\frac{1}{\frac{\text{1}}{\text{d}}-\frac{\text{f}}{{{\text{d}}^{\text{2}}}}}.\)
Đặt \(\text{y}=-\frac{\text{f}}{{{\text{d}}^{\text{2}}}}+\frac{\text{1}}{\text{d}},\) ta có L nhỏ nhất khi y lớn nhất.
Ta có y là hàm số bậc hai \(\left( \text{a}=-\text{f},\text{ b}=1 \right)\) với biến số là \(\frac{\text{1}}{\text{d}}\) và có a < 0 nên y có giá trị lớn nhất khi \(\frac{\text{1}}{\text{d}}=-\frac{\text{b}}{\text{2a}}=\frac{\text{1}}{\text{2f}}\Rightarrow \text{d}=\text{2f}.\)
Vị trí của ảnh: \(\text{d }\!\!'\!\!\text{ }=\frac{\text{d}.f}{\text{d}-f}=2\text{f}\text{.}\)
Khoảng cách ngắn nhất giữa vật thật và ảnh thật là L = 2f + 2f = 4f.