Trắc nghiệm Hàm số liên tục Toán Lớp 11

Câu 1:

Cho dãy số \(\left(u_{n}\right) \text { với } u_{n}=\frac{n}{4^{n}} \text { và } \frac{u_{n+1}}{u_{n}}<\frac{1}{2}\). Chọn giá trị đúng của \(\lim u_n\) trong các số sau: 

Câu 2:

Giá trị của \(A=\lim \frac{n-2 \sqrt{n}}{2 n}\) bằng 

Câu 3:

Giá trị của \(C=\lim \frac{\sqrt{n^{2}+1}}{n+1}\) bằng:

Câu 4:

Giá trị của \(B=\lim \frac{2 n+3}{n^{2}+1}\) bằng: 

Câu 5:

Giá trị của \(A=\lim \frac{2 n+1}{n-2}\) bằng 

Câu 6:

Giá trị của \(\lim \frac{2-n}{\sqrt{n+1}}\) bằng:

Câu 7:

Giá trị của \(\lim \frac{3 n^{3}+n}{n^{2}}\) bằng: 

Câu 8:

Giá trị của \(\lim \frac{\sqrt{n+1}}{n+2}\) bằng:

Câu 9:

Giá trị của \(\lim \frac{\cos n+\sin n}{n^{2}+1}\) bằng: 

Câu 10:

Giá trị của \(\lim \frac{2}{n+1}\) bằng:

Câu 11:

Giá trị của \(\lim \frac{1-n^{2}}{n}\) bằng: 

Câu 12:

Giá trị của \(\lim (2 n+1)\) bằng: 

Câu 13:

Giá trị của \(\lim \frac{\sin ^{2} n}{n+2}\) bằng: 

Câu 14:

Giá trị của \(\lim \frac{1}{n^{k}}\left(k \in \mathbb{N}^{*}\right)\) bằng: 

Câu 15:

Giá trị của \(\lim \frac{1}{n+1}\)bằng: 

Câu 16:

Hàm số \( f(x) = \sqrt {3 - x} + \frac{1}{{x + 4}}\) liên tục trên:

Câu 17:

Cho hàm số \( f(x) = \frac{{{x^2} + 1}}{{{x^2} + 5x + 6}}\). Hàm số f( x) liên tục trên khoảng nào sau đây?

Câu 18:

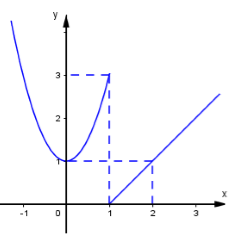
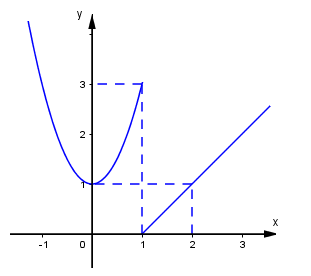
Cho hàm số y = f( x) có đồ thị như hình vẽ, chọn kết luận đúng:

Câu 19:

Hàm số y = f( x ) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?

Câu 20:

Tìm m để các hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt {x + 1} - 1}}{x}{\rm{ \ khi \ }}x > 0\\ 2{x^2} + 3m + 1{\rm{ \ khi \ }}x \le 0 \end{array} \right.\) liên tục trên R.

Câu 21:

Tìm m để các hàm số \(f(x) = \left\{ \begin{array}{l} \sqrt {2x - 4} + 3{\rm{ \ khi \ }}x \ge 2\\ \frac{{x + 1}}{{{x^2} - 2mx + 3m + 2}}{\rm{ \ khi \ }}x < 2 \end{array} \right.\) liên tục trên R.

Câu 22:

Tìm m để các hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}}{\rm{ \ khi \ }}x \ne 1\\ 3m - 2{\rm{ \ khi \ }}x = 1 \end{array} \right.\) liên tục trên R.

Câu 23:

Xác định a, b để các hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\,\sin x\,\,{\rm{khi }}\,\left| x \right| \le \frac{\pi }{2}}\\ {ax + b\,\,\,{\rm{khi}}\,\,\left| x \right| > \frac{\pi }{2}} \end{array}} \right.\) liên tục trên R.

Câu 24:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} \frac{{3 - \sqrt {9 - x} }}{x}{\rm{ , }}0 < x < 9\\ m{\rm{ , }}x = 0\\ \frac{3}{x}{\rm{ , }}x \ge 9 \end{array} \right.\). Tìm m để f(x) liên tục trên \(\left[ {0; + \infty } \right)\).

Câu 25:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} \frac{{{x^2} - 3}}{{x - \sqrt 3 }}{\rm{ ,\ }}x \ne \sqrt 3 \\ 2\sqrt 3 {\rm{ ,\ }}x = \sqrt 3 \end{array} \right.\). Tìm khẳng định đúng trong các khẳng định sau:           

(I) f(x) liên tục tại \(x = \sqrt3\)

(II) f(x) gián đoạn tại \(x = \sqrt3\)

(III) f(x) liên tục tại R

Câu 26:

Tìm a để các hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt {3x + 1} - 2}}{{{x^2} - 1}}{\rm{ \ khi \ }}x > 1\\ \frac{{a({x^2} - 2)}}{{x - 3}}{\rm{ \ khi \ }}x \le 1 \end{array} \right.\) liên tục tại x = 1

Câu 27:

Tìm a để các hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt {4x + 1} - 1}}{{a{x^2} + (2a + 1)x}}{\rm{ \ khi \ }}x \ne 0\\ 3{\rm{ \ khi \ }}x = 0{\rm{ }} \end{array} \right.\) liên tục tại x = 0

Câu 28:

Tìm a để các hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\,x + 2a\,\,{\rm{khi }}\,x < 0}\\ {{x^2} + x + 1\,\,\,{\rm{khi}}\,\,x \ge 0} \end{array}} \right.\) liên tục tại x = 0

Câu 29:

Cho hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{{x^2} - x - 2}}{{\sqrt {x - 2} }} + 2x{\rm{ \ khi \ }}x > 2\\ {x^2} - x + 3{\rm{ \ khi \ }}x \le 2 \end{array} \right.\). Khẳng định nào sau đây đúng nhất?

Câu 30:

Cho hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt[3]{x} - 1}}{{x - 1}}{\rm{ \ khi \ }}x \ne 1\\ \frac{1}{3}{\rm{ \ khi \ }}x = 1 \end{array} \right.\). Khẳng định nào sau đây đúng nhất?

Câu 31:

Cho hàm số \(f(x) = \left\{ \begin{array}{l} \dfrac{{x + 1 + \sqrt[3]{{x - 1}}}}{x}{\rm{ \ khi \ }}x \ne 0\\ 2{\rm{ \ khi \ }}x = 0 \end{array} \right.\). Khẳng định nào sau đây đúng nhất?

Câu 32:

Cho hàm số \(f(x) = \left\{ \begin{array}{l} \dfrac{{\sqrt x - 2}}{{x - 4}}{\rm{ \ khi \ }}x \ne 4\\ \dfrac{1}{4}{\rm{ \ khi \ }}x = 4 \end{array} \right.\). Khẳng định nào sau đây đúng nhất?

Câu 33:

Cho hàm số y = f(x) xác định trên R và \(\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = a,\;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = b\). Tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng

Câu 34:

Cho hàm số \(f\left( x \right)\; = \left\{ {\begin{array}{*{20}{l}}
{\frac{{x + \sqrt {x + 2} }}{{x + 1}}\;\;khi\;x > \; - 1\;}\\
{2x + 3\;\;\;\;\;\;\;\;\;\;\;\;khi\;x\; \le  - 1}
\end{array}} \right.\). Khẳng định nào sau đây đúng nhất.

Câu 35:

Chọn giá trị f(0) để các hàm số \(f\left( x \right)\; = \frac{{\sqrt[3]{{2x + 8}} - 2}}{{\sqrt {3x + 4}  - 2}}\) liên tục tại điểm x = 0

Câu 36:

Chọn giá trị f(0) để các hàm số \(f\left( x \right)\; = \;\frac{{\sqrt {2x + 1}  - 1}}{{x\left( {x + 1} \right)}}\) liên tục tại điểm x = 0.

Câu 37:

Cho hàm số \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} - 3x + 2}}{{\sqrt {x - 1} }} + 2\;\;khi\;x\; > \;1}\\
{3{x^2} + x - 1\;\;\;\;\;\;\;\;\;\;khi\;x \le 1}
\end{array}} \right.\). Khẳng định nào sau đây đúng nhất 

Câu 38:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
{\left( {x + 1} \right)^2},\,\,x > 1\\
{x^2} + 3,\,\,x < 1\\
{k^2},\,\,\,x = 1
\end{array} \right.\). Tìm k để f(x) gián đoạn tại x = 1.

Câu 39:

Cho hàm số \(f\left( x \right)\; = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sin \;5x}}{{5x}}\;\;\;x \ne 0}\\
{a + 2\;\;\;\;\;\;\;\;x = 0}
\end{array}} \right.\). Tìm a để f(x) liên tục tại x = 0.

Câu 40:

Cho hàm số \(f\left( x \right)\; = \left\{ {\begin{array}{*{20}{l}}
{\sqrt {4 - {x^2}} \;\;\;\; - 2 \le x \le 2\;}\\
{1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x\; > \;2}
\end{array}} \right.\). Tìm khẳng định đúng trong các khẳng định sau:

(I) f(x) không xác định tại x = 3

(II) f(x) liên tục tại x = -2

(III) \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 2\)

Câu 41:

Cho hàm số \(f\left( x \right)\; = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sqrt {2x + 8}  - 2}}{{\sqrt {x + 2} }}\;\;\;\;x >  - 2}\\
{0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x =  - 2}
\end{array}} \right.\). Tìm khẳng định đúng trong các khẳng định sau:

(I) \(\mathop {\lim }\limits_{x \to  - {2^ + }} f\left( x \right) = 0\)

(II) f(x) liên tục tại x = - 2

(III) f(x)gián đoạn tại x = - 2

Câu 42:

Cho hàm số \(f\left( x \right) = \frac{{\sqrt x  - 1}}{{x - 1}}\). Tìm khẳng định đúng trong các khẳng định sau:

(I) f(x) gián đoạn tại x = 1

(II) f(x) liên tục tại  x = 1

(III) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \frac{1}{2}\)

Câu 43:

Cho hàm số: \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\sqrt {\frac{{{x^2} + 1}}{{{x^3} - x + 6}}} \;\;x \ne 3\;;\;x \ne 2}\\
{b + \sqrt 3 \;\;\;\;\;\;\;\;\;\;\;\;x = 3;\;b \in R}
\end{array}} \right.\). Tìm b để f(x) liên tục tại x = 3

Câu 44:

Cho hàm số \(f\left( x \right)\; = \sqrt {{x^2} - 4} \). Chọn câu đúng trong các câu sau: 

(I) f(x) liên tục tại x = 2.

(II) f(x) gián đoạn tại x = 2

(III) f(x) liên tục trên đoạn [-2; 2].

Câu 45:

Cho hàm số \(f\left( x \right)\; = \frac{{{x^2} - 1}}{{x + 1}}\) và f(2) = m² - 2 với  x ≠ 2. Giá trị của m để f(x) liên tục tại x = 2 là:

Câu 46:

Cho hàm số: \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{3x - 5\;,\,\,\,x \le  - 2}\\
{ax - 1,\,\,\,x >  - 2}
\end{array}} \right.\)

Với giá trị nào của a thì hàm số f(x) liên tục tại x = - 2?

Câu 47:

Cho hàm số: \(f\left( x \right) = \frac{{\sqrt {x + 2}  - \sqrt {2 - x} }}{x},x \ne 0\)

Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x = 0?

Câu 48:

Cho hàm số: \(f\left( x \right) = \frac{{2x - 1}}{{{x^3} - 4x}}\)

Kết luận nào sau đây là đúng?

Câu 49:

Cho hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}
{x^2} - 5x,\,\,\,x >  - 1\\
{x^3} - 4x - 1,\,\,\,x <  - 1
\end{array} \right.\)

Kết luận nào sau đây không đúng?