Trắc nghiệm Hàm số liên tục Toán Lớp 11

Câu 1:

Tìm các giá trị của tham số m để hàm số \(f(x)=\left\{\begin{array}{ccc} \frac{x^{2}-3 x+2}{x^{2}-2 x} & \text { nếu } & x<2 \\ m x+m+1 & \text { nếu } & x \geq 2 \end{array}\right.\) liên tục trên \(\mathbb{R}\).

Câu 2:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{a x^{2}-(a-2) x-2}{\sqrt{x+3}-2} & \text { khi } x \neq 1 \\ 8+a^{2} & \text { khi } x=1 \end{array}\right.\). Có tất cả bao nhiêu giá trị của a để hàm số liên tục tại x=1?

Câu 3:

Tìm m để các hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt[3]{x-2}+2 x-1}{x-1} & \text { khi } x \neq 1 \\ 3 m-2 & \text { khi } x=1 \end{array}\right.\) liên tục trên  \(\mathbb{R}\)?

Câu 4:

Cho hàm số \(f(x)=\left\{\begin{array}{lr} \frac{\sqrt{4 x+1}-1}{a x^{2}+(2 a+1) x} & \text { khi } x \neq 0 \\ 3 & \text { khi } x=0 \end{array}\right.\) Tìm giá trị của a để hàm số f(x) liên tục tại \(x_{0}=0\)

Câu 5:

Hàm số \(f(x)=\left\{\begin{array}{ll} 3 & \text { khi } x=-1 \\ \frac{x^{4}+x}{x^{2}+x} & \text { khi } x \neq-1, x \neq 0 \\ 1 & \text { khi } x=0 \end{array}\right.\) liên tục tại:

Câu 6:

Biết rằng\(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\). Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{1+\cos x}{(x-\pi)^{2}} & \text { khi } x \neq \pi \\ m & \text { khi } x=\pi \end{array}\right.\) liên tục tại \(x=\pi\)?

Câu 7:

Biết rằng\(\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1\) . Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sin \pi x}{x-1} & \text { khi } x \neq 1 \\ m & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1 ?

Câu 8:

Biết rằng \(\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1\). Hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\tan x}{x} & \text { khi } x \neq 0 \\ 0 & \text { khi } x=0 \end{array}\right.\) liên tục trên khoảng nào sau đây? 

Câu 9:

Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} x^{2} \sin \frac{1}{x} & \text { khi } x \neq 0 \\ m & \text { khi } x=0 \end{array}\right.\) liên
tục tại x = 0. 

Câu 10:

Biết rằng hàm số \(f(x)=\left\{\begin{array}{ll} \frac{3-x}{\sqrt{x+1}-2} & \text { khi } x \neq 3 \\ m & \text { khi } x=3 \end{array}\right.\) liên tục tại x = 3 (với m là tham số). Khẳng định nào dưới đây đúng? 

Câu 11:

Tìm giá trị thực của tham số k để hàm số \(y=f(x)=\left\{\begin{array}{ll} \frac{\sqrt{x}-1}{x-1} & \text { khi } x \neq 1 \\ k+1 & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1. 

Câu 12:

Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{3}-x^{2}+2 x-2}{x-1} & \text { khi } x \neq 1 \\ 3 x+m & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1. 

Câu 13:

Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-x-2}{x-2} & \text { khi } x \neq 2 \\ m & \text { khi } x=2 \end{array}\right.\) liên tục tại x=2

Câu 14:

Cho hàm số f (x) xác định và liên tục trên \((-4 ;+\infty) \text { với } f(x)=\frac{x}{\sqrt{x+4}-2}\) với x ≠ 0 . Tính f(0)?

Câu 15:

Cho hàm số f(x) xác định và liên tục trên [-3;3] với \(f(x)=\frac{\sqrt{x+3}-\sqrt{3-x}}{x}\)với x ≠ 0 . Tính f(x)?

Câu 16:

Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \text { với } f(x)=\frac{x^{2}-3 x+2}{x-1}\) với mọi \(x \neq 1 . \text { Tính } f(1)\).

Câu 17:

\(\text { Hàm số } f(x)=\frac{x^{3}+x \cos x+\sin x}{2 \sin x+3} \text { liên tục trên: }\)

Câu 18:

\(\text { Hàm số } f(x)=\sqrt{3-x}+\frac{1}{\sqrt{x+4}} \text { liên tục trên: }\)

Câu 19:

Cho hàm số \(f(x)=\left\{\begin{array}{l} \frac{x^{3}-8}{x-2} \text { khi } x \neq 2 \\ m x+1 \text { khi } x=2 \end{array}\right.\). Tìm tất cả các giá trị của tham số thực m để hàm số liên tục tại x = 2 

Câu 20:

Cho hàm số \(f(x)=\left\{\begin{array}{l} 3 x+2 \text { khi } x<-1 \\ x^{2}-1 \text { khi } x \geq-1 \end{array}\right.\). Chọn khẳng định đúng trong các khẳng định sau. 

Câu 21:

Cho hàm số \(\begin{equation} f(x)=\frac{x-2}{x^{2}-3 x+2} \end{equation}\) . Hàm số liên tục trên 

Câu 22:

Cho hàm số \(\begin{equation} f(x)=\frac{x^{2}+1}{x^{2}+5 x+6} \end{equation}\). Hàm số f (x) liên tục trên khoảng nào sau đây? 

Câu 23:

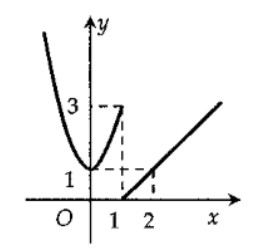
Hàm số y=f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu? 

Câu 24:

Phương trình x⁴ - 3x² + 1 = 0

Câu 25:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 3x + 2}}{{{x^2} + x}}\,neu\,x \ne  - 1\\3x + a\,neu\,x =  - 1\end{array} \right.\)

Với giá trị nào của tham số a thì hàm số f(x) liên tục tại x = -1?

Câu 26:

Cho hàm số f(x) xác định trên khoảng K chứa a. Hàm số f(x) liên tục tại x = a nếu:

Câu 27:

Tìm giá trị của tham số \(m\) để hàm số

\(f\left( x \right) = \left\{ \matrix{
{{\sqrt x - 1} \over {{x^2} - 1}},\,\,{\rm{ nếu }}\,\,x \ne 1 \hfill \cr 
{m^2}{\rm{ ,\,\, nếu }}\,\,x = 1 \hfill \cr} \right.\)  liên tục trên \(\left( {0; + \infty } \right)\).

Câu 28:

Cho hàm số \(f(x)=2 \sin x+3 \tan 2 x\). Khẳng định nào sau đây đúng nhất?

Câu 29:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} a^{2} x^{2} \,\,\,\,\,\,\,\,\,\,\,\,, x \leq \sqrt{2}, a \in \mathbb{R} \\ (2-a) x^{2}, x>\sqrt{2} \end{array}\right.\). Giá trị của a để f (x)  liên tục trên \(\mathbb{R}\) là 

Câu 30:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\tan x}{x}, & x \neq 0 \wedge x \neq \frac{\pi}{2}+k \pi, k \in \mathbb{Z} \\ 0 & , x=0 \end{array}\right.\). Hàm số y=f(x) liên tục trên các khoảng
nào sau đây?

Câu 31:

Cho hàm số \(f(x)=\left\{\begin{array}{l} \frac{\sqrt[3]{x}-1}{\sqrt{x}-1} \quad \text { khi } x>1 \\ \frac{\sqrt[3]{1-x}+2}{x+2} \text { khi } x \leq 1 \end{array}\right.\). Khẳng định nào sau đây đúng nhất.

Câu 32:

Cho hàm số \(f(x)=\left\{\begin{array}{cc} \frac{x^{2}-5 x+6}{2 x^{3}-16} & \text { khi } x<2 \\ 2-x & \text { khi } x \geq 2 \end{array}\right.\). Khẳng định nào sau đây đúng nhất. 

Câu 33:

Cho hàm số \(f(x)=\frac{x^{2}+1}{x^{2}+5 x+6}\).Khi đó hàm số \(f(x)\) liên tục trên các khoảng nào sau đây? 

Câu 34:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{3-\sqrt{9-x}}{x} & , 0<x<9 \\ m & , x=0 \\ \frac{3}{x} & , x \geq 9 \end{array}\right.\). Tìm m để f(x) liên tục trên \([0 ;+\infty)\) là?

Câu 35:

Tìm a để các hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt{3 x+1}-2}{x^{2}-1} & \text { khi } x>1 \\ \frac{a\left(x^{2}-2\right)}{x-3} & \text { khi } x \leq 1 \end{array}\right.\)liên tục tại x=1

Câu 36:

Tìm a để các hàm số \(f(x)=\left\{\begin{array}{lr} \frac{\sqrt{4 x+1}-1}{a x^{2}+(2 a+1) x} & \text { khi } x \neq 0 \\ 3 & \text { khi } x=0 \end{array}\right.\) liên tục tại x=0

Câu 37:

Tìm a để các hàm số \(f(x)=\left\{\begin{array}{c} x+2 a \text { khi } x<0 \\ x^{2}+x+1 \text { khi } x \geq 0 \end{array}\right.\) liên tục tại x=0.

Câu 38:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-x-2}{\sqrt{x-2}}+2 x & \text { khi } x>2 \\ x^{2}-x+3 & \text { khi } x \leq 2 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?

Câu 39:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt[3]{x}-1}{x-1} & \text { khi } x \neq 1 \\ \frac{1}{3} & \text { khi } x=1 \end{array}\right.\) . Khẳng định nào sau đây đúng nhất?

Câu 40:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x+1+\sqrt[3]{x-1}}{x} & \text { khi } x \neq 0 \\ 2 & \text { khi } x=0 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?

Câu 41:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x+\sqrt{x+2}}{x+1} & \text { khi } x>-1 \\ 2 x+3 & \text { khi } x \leq-1 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?

Câu 42:

Chọn giá trị f (0) để các hàm số \(f(x)=\frac{\sqrt[3]{2 x+8}-2}{\sqrt{3 x+4}-2}\) liên tục tại điểm x=0.

Câu 43:

Chọn giá trị f (0) để các hàm số \(f(x)=\frac{\sqrt{2 x+1}-1}{x(x+1)}\) liên tục tại điểm x=0
 

Câu 44:

Cho hàm số  \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-3 x+2}{\sqrt{x-1}}+2 & \text { khi } x>1 \\ 3 x^{2}+x-1 & \text { khi } x \leq 1 \end{array}\right.\) . Khẳng định nào sau đây đúng nhất 

Câu 45:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt{x}-2}{x-4} & \text { khi } x \neq 4 \\ \frac{1}{4} & \text { khi } x=4 \end{array}\right.\). Khẳng định nào sau đây đúng?

Câu 46:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} (x+1)^{2} & , x>1 \\ x^{2}+3 & , x<1 \\ k^{2} & , x=1 \end{array}\right.\). Tìm k để \(f(x)\) gián đoạn tại x=1

Câu 47:

Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sin 5 x}{5 x} & x \neq 0 \\ a+2 & x=0 \end{array}\right.\). Tìm a để \(f(x)\) liên tục tại x=0

Câu 48:

Giới hạn dãy số \(\left(u_{n}\right) \text { với } u_{n}=\frac{3 n-n^{4}}{4 n-5}\) là: 

Câu 49:

Giá trị của \(\lim \frac{-n^{2}+2 n+1}{\sqrt{3 n^{4}+2}}\) bằng:

Câu 50:

Kết quả đúng của \(\lim \left(5-\frac{n \cos 2 n}{n^{2}+1}\right)\) là