Trắc nghiệm Khái niệm về mặt tròn xoay Toán Lớp 12
-
Câu 1:
Tính thể tích của khối trụ có bán kính đáy \(r = \sqrt 3 \) và chiều cao h = 4.
-
Câu 2:
Cắt một khối trụ cho trước bởi một mặt phẳng vuông góc với trục thì được hai khối trụ mới có tổng diện tích toàn phần nhiều hơn diện tích toàn phần của khối trụ ban đầu \(18\pi \,\left( {d{m^2}} \right)\). Biết chiều cao của khối trụ ban đầu là \(5\,\left( {dm} \right)\), tính tổng diện tích toàn phần S của hai khối trụ mới.
-
Câu 3:
Một hình trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R. Diện tích xung quanh của hình trụ bằng:
-
Câu 4:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = A{\rm{D}} = 2{\rm{a}}, AA’ = 3a\sqrt 2 \). Tính diện tích toàn phần S của hình trụ có hai đáy lần lượt ngoại tiếp hai đáy của hình hộp chữ nhật đã cho.
-
Câu 5:
Một hình trụ có bán kính đáy \(r = 5{\rm{cm}}\), chiều cao \(h = 7{\rm{cm}}\). Tính diện tích xung quang của hình trụ.
-
Câu 6:
Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Tính diện tích xung quanh của hình trụ.
-
Câu 7:
Một hình trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông. Tính diện tích toàn phần của hình trụ đó.
-
Câu 8:
Tính diện tích xung quanh S của hình trụ có bán kính bằng 3 và chiều cao bằng 4.
-
Câu 9:
Cho hình trụ có bán kính đáy bằng a và độ dài đường cao bằng 3a. Diện tích toàn phần hình trụ đã cho bằng:
-
Câu 10:
Tính diện tích xung quanh của một hình trụ có chiều cao \(20\;{\rm{m}}\), chu vi đáy bằng \(5\;{\rm{m}}\).
-
Câu 11:
Hình trụ có bán kính đáy bằng a và chiều cao bằng \(a\sqrt 3 \). Khi đó diện tích toàn phần của hình trụ bằng
-
Câu 12:
Diện tích xung quanh của mặt trụ có bán kính đáy R, chiều cao h là
-
Câu 13:
Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy r và độ dài đường sinh \(l\) bằng:
-
Câu 14:
Cho khối trụ \(\left( T \right)\) có bán kính đáy R = 1, thể tích \(V = 5\pi \). Tính diện tích toàn phần của hình trụ tương ứng
-
Câu 15:
Cho hình trụ có bán kính đáy \(r = 5\left( {{\rm{cm}}} \right)\) và khoảng cách giữa hai đáy bằng \(7\left( {{\rm{cm}}} \right)\). Diện tích xung quanh của hình trụ là
-
Câu 16:
Một hình trụ có bán kính đáy bằng r = 50cm và có chiều cao h = 50cm. Diện tích xung quanh của hình trụ bằng:
-
Câu 17:
Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7. Diện tích xung quanh của hình trụ đã cho bằng
-
Câu 18:
Cho hình trụ có bán kính đáy \(5\,cm\), chiều cao \(4\,cm\). Diện tích toàn phần của hình trụ này là
-
Câu 19:
Một hình trụ có bán kính đáy r = a, độ dài đường sinh \(l = 2a\). Diện tích toàn phần của hình trụ này là:
-
Câu 20:
Cho khối trụ có thể tích V và bán kính R. Tìm chiều cao h của khối trụ đó.
-
Câu 21:
Một khối trụ có thể tích bằng \(16\pi .\) Nếu chiều cao khối trụ tăng lên hai lần và giữ nguyên bán kính đáy thì được khối trụ mới có diện tích xung quanh bằng \(16\pi .\) Bán kính đáy của khối trụ ban đầu là
-
Câu 22:
Cho hình trụ có diện tích xung quanh bằng \(16\pi {a^2}\) và độ dài đường sinh bằng 2a. Tính bán kính r của đường tròn đáy của hình trụ đã cho.
-
Câu 23:
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Câu 24:
Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Tính thể tích khối trụ.
-
Câu 25:
Khối trụ tròn xoay có thể tích bằng \(144\pi \) và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng
-
Câu 26:
Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là:
-
Câu 27:
Một hình trụ có diện tích xung quanh bằng \(4\pi {a^2}\) và bán kính đáy là a. Tính độ dài đường cao của hình trụ đó.
-
Câu 28:
Cho hình trụ có diện tích xung quanh bằng \(2{\rm{\pi }}{a^2}\) và bán kính đáy bằng a. Độ dài đường sinh của hình trụ đã cho bằng
-
Câu 29:
Trong không gian, cho hai điểm phân biệt A, B và số thực dương k. Tập hợp các điểm M sao cho diện tích tam giác MAB bằng k là:
-
Câu 30:
Cho đường thẳng d cố định. Đường thẳng \(\Delta \) song song với d và cách d một khoảng không đổi. Xác định mặt tròn xoay tạo thành khi quay \(\Delta \) quanh d.
-
Câu 31:
Mệnh đề nào sau đây là sai?
-
Câu 32:
Cho đường thẳng \({d_2}\) cố định, đường thẳng \({d_1}\) song song và cách \({d_2}\) một khoảng cách không đổi. Khi \({d_1}\) quay quanh \({d_2}\) ta được
-
Câu 33:
Gọi \(l, h, R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức luôn đúng là
-
Câu 34:
Khi quay một hình chữ nhật và các điểm trong của nó quanh trục là một đường trung bình của hình chữ nhật đó, ta nhận được hình gì?
-
Câu 35:
Một hình trụ có diện tích xung quanh bằng \(4\pi \) và có chiều cao bằng đường kính đáy. Thể tích khối trụ tương ứng bằng
-
Câu 36:
Cho hình chữ nhật ABCD có AB = a và góc \(BDC = {30^0}\). Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là
-
Câu 37:
Cho hình vuông ABCD cạnh \(8\,(cm)\). Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:
-
Câu 38:
Một hình trụ có bán kính đáy \(r = 5\,(cm)\), chiều cao \(r = 7\,(cm)\). Diện tích xung quanh của hình trụ này là:
-
Câu 39:
Hình nón có bán kính đáy là 4a, chiều cao là 3a có diện tích xung quanh bằng:
-
Câu 40:
Cho hình nón có đường cao bằng 2a và đường sinh bằng \(a\sqrt 5 \). Tính diện tích toàn phần của hình nón.
-
Câu 41:
Cho khối nón có bán kính đáy và đường sinh lần lượt là r = 3cm,l = 5cm. Tính thể tích khối nón.
-
Câu 42:
Cho hình nón có bán kính đáy và đường cao lần lượt là r = 6cm,h = 8cm. Tính diện tích toàn phần của hình nón.
-
Câu 43:
Cho hình nón có bán kính đáy và đường cao lần lượt là r = 3cm,h = 4cm. Tính diện tích xung quanh của hình nón.
-
Câu 44:
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a . Tính diện tích toàn phần của hình trụ đã cho.
-
Câu 45:
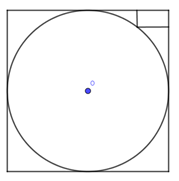
Cho hình trụ (T) có ( C ), (C') ) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước 1 x 2 (như hình vẽ dưới đây). Thể tích của khối trụ (T) là
-
Câu 46:
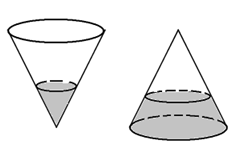
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?
-
Câu 47:
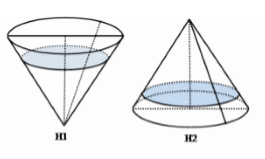
Một khối đồ chơi có dạng khối nón, chiều cao bằng (20cm ), trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng \(\frac{2}{3}\) chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao (h ) của lượng nước trong khối đó gần với giá trị nào sau đây?
-
Câu 48:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông cạnh a và cạnh bên bằng 2a Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A'B'C'D' và đáy là hình tròn nội tiếp hình vuông ABCD là:
-
Câu 49:
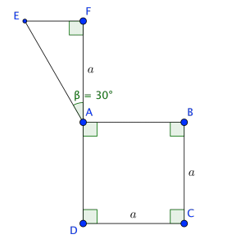
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục (DF )
-
Câu 50:
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng