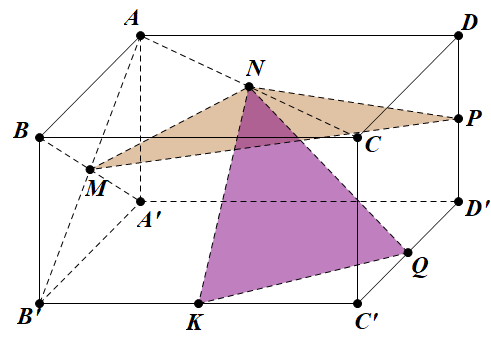
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có các cạnh bằng 2 , gọi điểm M là tâm của mặt bên \(A B B^{\prime} A^{\prime}\), các điểm N, P, Q, K lần lượt là trung điểm của các cạnh \(A C, D D^{\prime}, D^{\prime} C^{\prime}, B^{\prime} C^{\prime}\) . Tính cos góc giữa hai mặt phẳng \((M N P) \text { và }(A Q K)\)?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa chọn hệ trục tọa độ Oxyz với gốc \(A^{\prime} \equiv O\)cạnh A B' nằm trên Ox , cạnh A' D' nằm trên Oy và cạnh A A' nằm trên Oz .
Từ các dữ kiện đề bài đã cho ta tìm được tọa độ các điểm
\(\begin{array}{l} M(1 ; 0 ; 1), N(1 ; 1 ; 2), P(0 ; 2 ; 1), K(2 ; 1 ; 0), Q(1 ; 2 ; 0), A(0 ; 0 ; 2) \\ \text { Ta có } \overrightarrow{M N}=(0 ; 1 ; 1), \overrightarrow{N P}=(-1 ; 1 ;-1), \overrightarrow{A K}=(2 ; 1 ;-2), \overrightarrow{A Q}=(1 ; 2 ;-2) . \end{array}\)
Gọi \(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\) lần lượt là 2 vector pháp tuyến của mặt phẳng \((M N P) \text { và }(A Q K)\).
Như vậy ta tính được \(\overrightarrow{u_{1}}(-2 ;-1 ; 1), \overrightarrow{u_{2}}(2 ; 2 ; 3)\) .
Ta gọi góc giữa hai mặt phẳng (MNP) và ( AQK) là \(\varphi .\) .
Như vậy \(\cos \varphi=\frac{\left|\vec{u}_{1} \cdot \overrightarrow{u_{2}}\right|}{\left|\overrightarrow{u_{1}}\right|\left|\overrightarrow{u_{2}}\right|}=\frac{|-2.2-1.2+1.3|}{\sqrt{2^{2}+1^{2}+1^{2}} \sqrt{2^{2}+2^{2}+3^{2}}}=\frac{\sqrt{102}}{34}\)