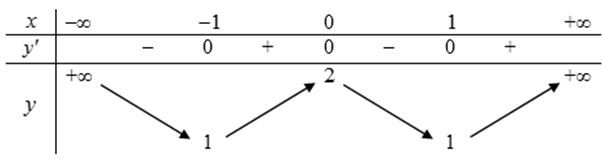
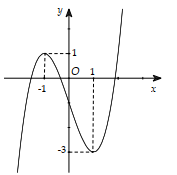
Biết rằng đồ thị hàm số \(y = {x^3} + 3{x^2}\) có dạng như hình vẽ:

Hỏi đồ thị hàm số \(y = \left| {{x^3} + 3{x^2}} \right|\) có bao nhiêu điểm cực trị?

Câu hỏi liên quan

• Hàm số \(y = - {x^4} + {x^2} + 3\) có bao nhiêu điểm cực trị?

• Biết đồ thị hàm số \(y=x^{3}-2 x^{2}+a x+b\) có điểm cực trị là A(1;3) . Khi đó giá trị của 4a-b là: 

• Cho hàm số \( y = mx⁴ + (2m +1)x² +1\). Tìm tất cả các giá trị thực của tham số  m để hàm số có đúng một điểm cực tiểu.

   

ZUNIA12

• Số điểm cực đại của hàm số \(f\left( x \right) = - 3{{\rm{x}}^4} - \frac{5}{2}{{\rm{x}}^2} - 1\) là

• Cho hàm số y =f(x) có đồ thị như hình dưới đây

  

  Số điểm cực trị của đồ thị hàm số \(y=|f(x)|\) là

• Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

  

  Khẳng định nào sau đây là khẳng định đúng?

• Cho hàm số \(y = f\left( x \right)\) liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như hình vẽ.

  

  Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?

• Điểm cực đại của đồ thị hàm số \(y = - {x^4} + 4{x^2} + 2\) là:

• Có tất cả bao nhiêu số nguyên m thuộc đoạn [-2017;2017] để hàm số \(y=\left|x^{3}-3 x^{2}+m\right|\) điểm cực trị?

• Hàm số \(y = \frac{1}{3}{x^3} + 2{x^2} + 3x – 1\) có các điểm cực trị là

• Cho hàm số y =  f (x) có bảng biến thiên như sau:

  

  Mênh đề nào dưới đây đúng?

   

• Điểm cực đại của hàm số \(y =  - {x^3} - 3{x^2} + 1\) là:

• Điểm cực đại của hàm số \(y = \frac{1}{4}{x^4} + 2{x^2} - 2\) là:

• Hàm số  y=f(x) có \(f'\left( x \right) = \left( { - x + 2} \right){\left( {x + 1} \right)^4}\left( {x - 3} \right)\) . Số điểm cực trị của hàm số là:

• Số cực trị của hàm số \(f\left( x \right) = {{\rm{x}}^4} + \frac{5}{4}{{\rm{x}}^2} - 12\) là

• Cho hàm số \(y=a x^{3}+b x^{2}+c x+d .\) . Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(-1;-1)  thì hàm số có phương trình là: 

• Cho hàm số \(y\; = \;{x^4}\; - 2{x^2}\; + 3\). Khẳng định nào sau đây là đúng?

• Hàm số  y=f(x) có \(f'\left( x \right) = \left( {3x + 5} \right){\left( {x - 1} \right)^2}\left( {{x^2} - 3} \right)\). Số điểm cực trị của hàm số là:

• Hàm số y = x³ – 3x + 2 đạt cực đại tại

• Hàm số \(y = {x^4} - 2{x^2} + 4\) có bao nhiêu điểm cực trị?