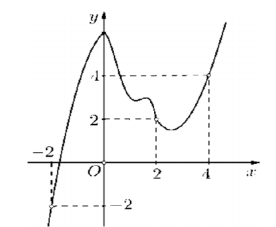
Cho hàm số f(x) , bảng biến thiên của hàm số f '(x) như sau:
Số cực trị của hàm số \(y=f\left(4 x^{2}-4 x\right)\) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ bảng biến thiên

Ta thấy \(f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{c} x=a \in(-\infty ;-1) \\ x=b \in(-1 ; 0) \\ x=c \in(0 ; 1) \\ x=d \in(1 ;+\infty) \end{array}\right.\)
Với \(y=f\left(4 x^{2}-4 x\right)\) ta có \(y^{\prime}=(8 x-4) f^{\prime}\left(4 x^{2}-4 x\right)\)
\(y^{\prime}=0 \Leftrightarrow\left[\begin{array}{c} 8 x-4=0 \\ f^{\prime}\left(4 x^{2}-4 x\right)=0 \end{array}\right.\)
\(\Leftrightarrow \left[\begin{array}{c} x=\frac{1}{2} \\ 4 x^{2}-4 x=a \in(-\infty ;-1)(1) \\ 4 x^{2}-4 x=b \in(-1 ; 0)(2) \\ 4 x^{2}-4 x=c \in(0 ; 1)(3) \\ 4 x^{2}-4 x=d \in(1 ;+\infty)(4) \end{array}\right.\)
Xét hàm số \(g(x)=4 x^{2}-4 x, \text { ta có } g^{\prime}(x)=8 x-4=0 \Leftrightarrow x=\frac{1}{2}\)
Bảng biến thiên

Từ bảng biến thiên của g(x) ta có:
Vì \(\begin{array}{l} a \in(-\infty ;-1) \end{array}\) nên (1) vô nghiệm.
Vì \(b \in(-1 ; 0) \) nên (2) có 2 nghiệm phân biệt.
Vì \(c \in(0 ; 1)\) nên (3) có 2 nghiệm phân biệt.
Vì \(d \in(1 ;+\infty)\) nên (4) có 2 nghiệm phân biệt.
Vậy hàm số \(y=f\left(4 x^{2}-4 x\right)\) có 7 điểm cực
.png)
.jpg.png)