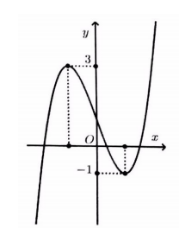
Cho hàm số y=f(x) có đồ thị y=f'(x) như hình vẽ sau
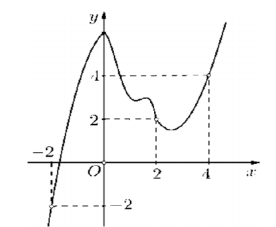
Đồ thị hàm số \(g(x)=\left|2 f(x)-x^{2}\right|\) có tối đa bao nhiêu điểm cực trị?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai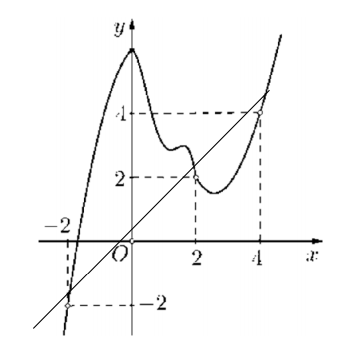
Xét hàm số \(h(x)=2 f(x)-x^{2} \Rightarrow h^{\prime}(x)=2 f^{\prime}(x)-2 x\)
Từ đồ thị ta thấy \(h^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=x \Leftrightarrow x=-2 \vee x=2 \vee x=4\)
\(\begin{array}{l} \int\limits_{-2}^{2}\left(2 f^{\prime}(x)-2 x\right) d x>\int\limits_{2}^{4}\left(2 x-2 f^{\prime}(x)\right) d x>0 \\ \left.\Leftrightarrow h(x)\right|_{-2} ^{2}>-\left.h(x)\right|_{2} ^{4} \Leftrightarrow h(2)-h(-2)>-(h(4)-h(2)) \Leftrightarrow h(4)>h(-2) \end{array}\)
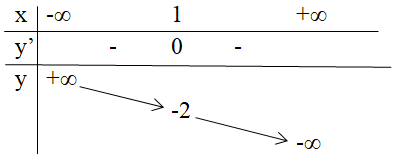
Bảng biến thiên
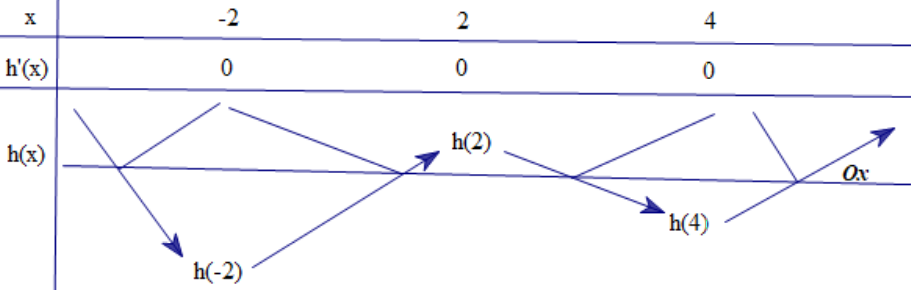
Vậy \(g(x)=\left|2 f(x)-x^{2}\right|\) có tối đa 7 cực trị
ADMICRO
YOMEDIA
ZUNIA9