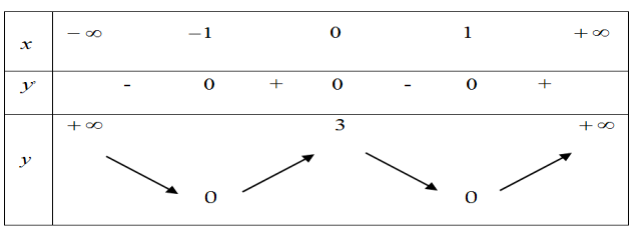
Cho hàm số y = x⁴-2mx²+2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A; B; C thỏa mãn OA.OB.OC = 12?

Câu hỏi liên quan

• Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} - 3m{x^2} + \left( {m - 1} \right)x + 2\) có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương

• Hàm số \(y = \frac{1}{3}{x^3} - \left( {m + 1} \right){x^2} + \left( {2{m^2} + 1} \right)x + m\) đạt cực tiểu tại x = 1 khi

• Gọi x₁, x₂ là hai điểm cực trị của hàm số \[y = \frac{{{x^2} - 4x}}{{x + 1}}\). Tính giá trị của biểu thức P = x₁.x₂

ZUNIA12

• Hàm số nào sau đây có số điểm cực trị ít nhất  so với số điểm cực trị của cáchàm số còn lại?

   

• Cho hàm số \(y = \frac{1}{2}x - \sqrt x \). Tìm khẳng định đúng?

• Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số  y = mx⁴ + (m² - 9)x² + 10 có ba điểm cực trị.

   

• Cho hàm số y =  f (x) có bảng biến thiên như sau

  

  Mệnh đề nào dưới đây sai?

   

• Tìm tất các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}+(m+3) x^{2}+4(m+3) x+m^{3}-m\) đạt cực trị tại \(x_{1}, x_{2}\) thỏa mãn \(-1<x_{1}<x_{2}\)

• Hàm số  y=f(x) có \(f'\left( x \right) = \frac{1}{2}{x^3}{\left( {x - 1} \right)^2}\left( {2x - 1} \right){\left( {x + 2} \right)^5}\) . Số điểm cực trị của hàm số là:

• Cho hàm số \(y=a x^{3}+b x^{2}+c x+d .\) . Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(-1;-1)  thì hàm số có phương trình là: 

• Số điểm cực đại của hàm số \(f\left( x \right) = \frac{1}{5}{{\rm{x}}^4} - \frac{4}{3}{{\rm{x}}^2} + 2\) là

• Tìm tập nghiệm của bất phương trình \(3 \sqrt{3-2 x}+\frac{5}{\sqrt{2 x-1}}-2 x \leq 6\) là

• Tìm điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x + 1\).

• Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = {x^3} - 3m{x^2} + 4{m^3}\) có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng (d): y = x 

• Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó.

  

• Tìm tất cả các điểm cực đại của hàm số y = - x⁴ + 2x² + 1

• x = 2 không phải là điểm cực đại của hàm số nào sau đây? 

• Hàm số \(y = – {x^4} + 8{x^2} – 7\) có bao nhiêu giá trị cực trị?

• Tìm tập hợp tất cả giá trị thực của tham số  m  để hàm số y = x⁴ - 2mx² + 2  có ba điểm cực trị

   

• Tìm tất cả các giá trị thực của tham số m để hàm số \(y=(m+1) x^{4}-m x^{2}+\frac{3}{2}\) chỉ có cực tiểu mà không có cực đại.