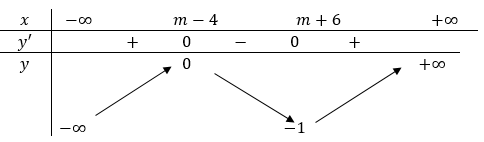
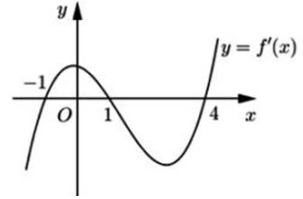
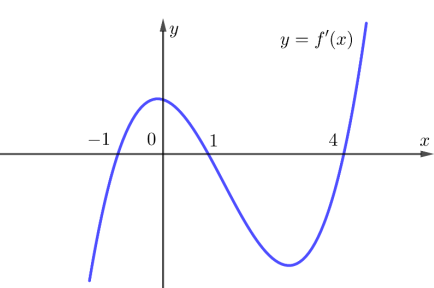
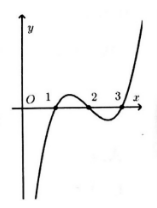
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = mf(x) = m có đúng hai nghiệm phân biệt.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Ta có \(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}
f\left( x \right),f\left( x \right) \ge 0\\
- f\left( x \right),f\left( x \right) < 0
\end{array} \right.\)
Từ đó suy ra cách vẽ đồ thị hàm số (C) như sau:
- Giữ nguyên đồ thị y = f (x) phía trên trục hoành.
- Lấy đối xứng phần đồ thị y = f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
Kết hợp hai phần ta được đồ thị hàm số y = |f(x) như hình vẽ.
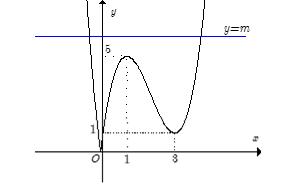
Phương trình |f(x)| = m là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m (cùng phương với trục hoành).
Dựa vào đồ thị, ta có ycbt ⇔ 0 < m < 1; m > 5.
Câu hỏi liên quan
-
Cho hàm số \(y = \sqrt {{x^2} – 1} \). Mệnh đề nào dưới đây đúng?
-
Tìm tất cả giá trị của m để hàm số \(y = \frac{{\left( {m + 1} \right)x - 2}}{{x - m}}\) đồng biến trên từng khoảng xác định
-
Tìm tất cả các giá trị của m để hàm số \(y=2^{x^{3}-x^{2}+m x}\) đồng biến trên \([1,2]\)
-
Cho hàm số y = x4 – 2x2 + 3. Tìm các khoảng đồng biến của hàm số
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
-
Hàm số nào sau đây đồng biến trên R?
-
Cho hàm số f x có bảng biến thiên như sau
Hàm số \(y=(f(x))^{3}-3(f(x))^{2}\) nghịch biến trên khoảng nào dưới đây?
-
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ bên. Hàm số \(y=f(2-x)\) đồng biến trên khoảng
-
Cho hàm số y=f(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
-
Hàm số \(y = {x^3} + 8{x^2} + 3x - 2\) đồng biến trên các khoảng:
-
Tìm tham số m thì hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-m+2\) đồng biến trên R?
-
Cho hàm số \(y = \frac{{\ln x – 4}}{{\ln x – 2m}}\) với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của S.
-
Có bao nhiêu số tự nhiên m không vượt quá 2020 và là số chẵn để hàm số \(y=\frac{2 m x+4}{x+2 m}\) đồng biến trên \((1 ;+\infty) ?\)
-
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
\(y = \frac{{2x + 1}}{{x + 1}}\) (I) ; y = - x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
-
Giá trị của tham số m để \(f(x)=2 m x^{3}-6 x^{2}+(2 m-4) x+3+m\) nghịch biến trên R là?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=x^{4}-2(m-1) x^{2}+m-2\) đồng biến trên khoảng (1;3)?
-
Với giá trị của tham số m để hàm số \(y=\frac{x+2}{x+5 m}\) đồng biến trên khoảng \((-\infty ;-10)\)
-
Hàm số nào sau đây đồng biến trên R.
-
Cho hàm số \(y = \frac{{mx – 2m – 3}}{{x – m}}\) với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.
-
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R, có đồ thị hàm số y=f′(x) như hình vẽ. Hỏi hàm số y=f(2x–5) đồng biến trong khoảng nào?
