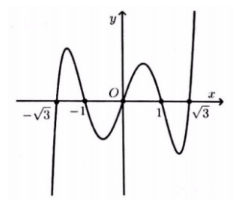
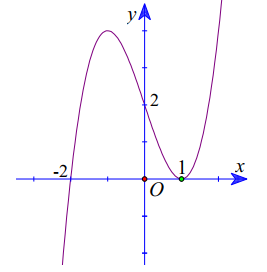
Cho hàm số y=f(x) xác định trên \(\mathbb{R}\)và hàm số y=f'(x) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \(y=f\left(x^{2}-3\right)\)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiQuan sát đồ thị ta có \(y=f^{\prime}(x)\) đổi dấu từ âm sang dương qua x=-2 nên hàm số y=f(x) có một điểm cực trị là x=-2 .
Ta có \(y^{\prime}=\left[f\left(x^{2}-3\right)\right]^{\prime}=2 x \cdot f^{\prime}\left(x^{2}-3\right)=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x^{2}-3=-2 \\ x^{2}-3=1 \end{array} \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=\pm 1 \\ x=\pm 2 \end{array}\right.\right.\)
Mà \(x=\pm 2\) là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số \(y=f\left(x^{2}-3\right)\) có ba cực trị.
ADMICRO
YOMEDIA
ZUNIA9