Cho \(x>y \geq 0\) thỏa mãn \(3^{x+y+2 x y-2}=\frac{2(1-x y)}{x+y}\) . Giá trị nhỏ nhất của biểu thức P=x+5 y là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{aligned} &\text { Điều kiện } 1-x y>0 \text { . } \\ &\text { Ta có: } 3^{x+y+2 x y-2}=\frac{2(1-x y)}{x+y} \Leftrightarrow x+y+2 x y-2=\log _{3} \frac{2(1-x y)}{x+y} . \\ &\Leftrightarrow \log _{3}[2(1-x y)]+2(1-x y)=\log _{3}(x+y)+(x+y)\left(^{*}\right) \\ &\text { Xét hàm } f(t)=t+\log _{3} t \text { với } t>0 \Rightarrow f^{\prime}(t)=1+\frac{1}{t \ln 3}>0 \end{aligned}\)
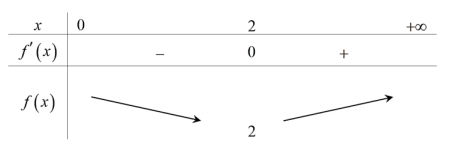
\(\begin{aligned} &\left(^{*}\right) \Leftrightarrow f(2(1-x y))=f(x+y) \Leftrightarrow 2(1-x y)=x+y \Leftrightarrow y=\frac{2-x}{2 x+1}\\ &\text { Khi đó } 1-x y>0 \Leftrightarrow \frac{x^{2}+1}{2 x+1}>0 \text { (luôn đúng). }\\ &\text { Ta có } P=x+5 y=x+5 \frac{2-x}{2 x+1} \text { . Đặt } f(x)=x+5 \frac{2-x}{2 x+1} \Rightarrow f^{\prime}(x)=1-\frac{25}{(2 x+1)^{2}} \text { . }\\ &f^{\prime}(x)=0 \Rightarrow x=2 . \end{aligned}\)
\(\text { Vậy } P_{M i n}=2 \text { đạt được khi }\left\{\begin{array}{l} x=2 \\ y=0 \end{array}\right. \text { . }\)