Đường thẳng \(\Delta \) đi qua điểm \(M\left( {3;\,1;\,1} \right)\), nằm trong mặt phẳng \(\left( \alpha \right):x + y – z – 3 = 0\) và tạo với đường thẳng \(d:\left\{ \begin{array}{l}x = 1\\y = 4 + 3t\\z = – 3 – 2t\end{array} \right.\) một góc nhỏ nhất thì phương trình của \(\Delta \) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai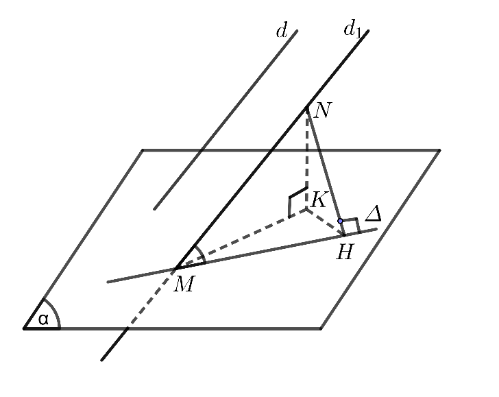
Đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {0;\,3;\, – 2} \right)\).
Mặt phẳng \(\left( \alpha \right)\) có vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,1;\, – 1} \right)\).
Vì \(\overrightarrow u .\overrightarrow n = 0.1 + 3.1 + \left( { – 2} \right).\left( { – 1} \right) = 5 \ne 0\) nên d cắt \(\left( \alpha \right)\).
Gọi \({d_1}\) là đường thẳng đi qua M và \({d_1}\) // d, suy ra \({d_1}\) có phương trình: \(\left\{ \begin{array}{l}x = 3\\y = 1 + 3t\\z = 1 – 2t\end{array} \right.\).
Lấy \(N\left( {3;\,4;\, – 1} \right) \in {d_1}\). Gọi K, H lần lượt là hình chiếu vuông góc của N trên mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \).
Ta có: \(\widehat {\left( {d,\Delta } \right)} = \widehat {NMH}\) và \(\sin \widehat {NMH} = \frac{{NH}}{{MN}} \ge \frac{{NK}}{{MN}}.\)
Do vậy \(\widehat {\left( {d,\Delta } \right)}\) nhỏ nhất khi \(K \equiv H\) hay \(\Delta \) là đường thẳng MK.
Đường thẳng NK có phương trình: \(\left\{ \begin{array}{l}x = 3 + t\\y = 4 + t\\z = – 1 – t\end{array} \right.\).
Tọa độ điểm K ứng với t là nghiệm của phương trình:
\(\left( {3 + t} \right) + \left( {4 + t} \right) – \left( { – 1 – t} \right) – 3 = 0 \Leftrightarrow t = – \frac{5}{3}\). Suy ra \(K\left( {\frac{4}{3};\,\frac{7}{3};\,\frac{2}{3}} \right)\).











