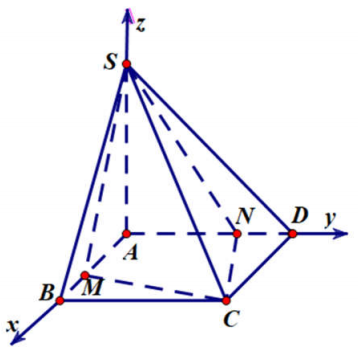
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA vuông góc với mặt phẳng đáy (ABCD) và SA = 2 . Gọi M , N lần lượt là hai điểm thay đổi trên hai cạnh AB , AD sao cho mặt phẳng (SMC) vuông góc với mặt phẳng (SNC) . Thể tích khối chóp S.AMCN đạt giá trị nhỏ nhất bằng ?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn hệ trục tọa độ Oxyz như hình vẽ trên sao cho\(A(0 ; 0 ; 0), B(2 ; 0 ; 0), D(0 ; 2 ; 0), S(0 ; 0 ; 2)\), suy ra \(C(2 ; 2 ; 0)\)
\(\begin{array}{l} \text { Đặt } A M=m, A N=n, m, n \in[0 ; 2], \text { suy ra } M(m ; 0 ; 0), N(0 ; n ; 0) \\ \overrightarrow{S M}=(m ; 0 ;-2), \overrightarrow{S C}=(2 ; 2 ;-2), \overrightarrow{S N}=(0 ; n ;-2) \\ \Rightarrow \overline{n_{(S M C)}}=[\overline{S M}, \overrightarrow{S C}]=(4 ; 2 m-4 ; 2 m), \overline{n_{(S N C)}}=[\overrightarrow{S N}, \overrightarrow{S C}]=(4-2 n ;-4 ;-2 n) \\ \text { Do }(S M C) \perp(S N C) \text { nên } \overline{n_{(S M C)} \cdot n_{(S N C)}}=0 \Leftrightarrow 4(4-2 n)-4(2 m-4)-4 m n=0 \\ \Leftrightarrow m n+2(m+n)=8 \end{array}\)
\(\begin{aligned} &\text { Mặt khác } m n+2(m+n) \leq\left(\frac{m+n}{2}\right)^{2}+2(m+n) \text { nên ta có } \frac{(m+n)^{2}}{4}+2(m+n)-8 \geq 0\\ &\Leftrightarrow\left[\begin{array}{l} m+n \geq 4 \sqrt{3}-4 \\ m+n \leq-4 \sqrt{3}-4 \end{array} . \text { Do } m, n \geq 0\right. \text { nên } m+n \geq 4 \sqrt{3}-4\\ &S_{A M C N}=S_{A B C D}-S_{B M C}-S_{D N C}=4-(2-m)-(2-n)=m+n \geq 4 \sqrt{3}-4\\ &V_{S . A M C D}=\frac{1}{3} S A \cdot S_{A M C N}=\frac{2}{3}(m+n) \geq \frac{8 \sqrt{3}-8}{3} \end{aligned}\)
Vậy thể tích nhỏ nhất của khối chóp S AMCN là \(\frac{8 \sqrt{3}-8}{3}\)