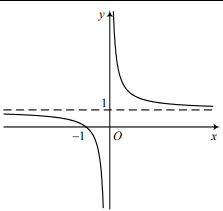
Số tiệm cận của đồ thị hàm số \(y=\frac{x^{2}+x-2}{(x+2)^{2}}\) là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTXĐ: \(D=\mathbb{R} \backslash\{-2\}\)
Trên TXĐ của hàm số, biến đổi được \(y=\frac{x-1}{x+2}\)
Ta có \(\lim\limits _{x \rightarrow+\infty} \frac{x-1}{x+2}=\lim\limits _{x \rightarrow-\infty} \frac{x-1}{x+2}=1 ; \lim\limits _{x \rightarrow-2^{+}} \frac{x-1}{x+2}=-\infty ; \lim\limits _{x \rightarrow-2^{-}} \frac{x-1}{x+2}=+\infty\)
Do đó đồ thị có 2 tiệm cận là y=1 và x=-2
ADMICRO
YOMEDIA
ZUNIA9
.png)