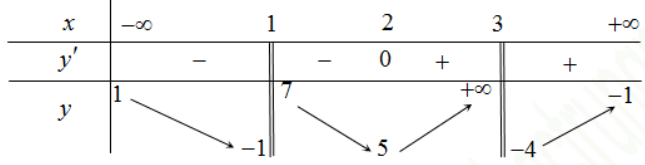Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+4}-2}{x^{2}+x}\) là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTXĐ: \(D=[-4 ;+\infty) \backslash\{0 ;-1\}\)
Ta có : \(\mathop {\lim }\limits_{x \to 0} y = \frac{1}{4}\) nên x=0 không là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} y = \mathop {\lim }\limits_{x \to {{( - 1)}^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = + \infty \\ \mathop {\lim }\limits_{x \to {{( - 1)}^ - }} y = \mathop {\lim }\limits_{x \to {{( - 1)}^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = - \infty \)
\(\Rightarrow \mathrm{TCD}: x=-1\)
Vậy đồ thị hàm số có 1 tiệm cận đứng.
ADMICRO
YOMEDIA
ZUNIA9

.png)