Tìm m để hàm số \(y=-x^{3}-m x+\frac{3}{28 x^{7}}\) nghịch biến trên \((0 ;+\infty) \text { . }\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y^{\prime}=-3 x^{2}-m-\frac{3}{4 x^{8}}\)
\(\text { Hàm số } y=-x^{3}-m x+\frac{3}{28 x^{7}} \text { nghịch biến trên }(0 ;+\infty) \Leftrightarrow y^{\prime} \leq 0, \forall x \in(0 ;+\infty)\)
\(\begin{array}{l} \Leftrightarrow-3 x^{2}-m-\frac{3}{4 x^{8}} \leq 0, \forall x \in(0 ;+\infty) \\ \Leftrightarrow-3 x^{2}-\frac{3}{4 x^{8}} \leq m, \quad \forall x \in(0 ;+\infty) \\ \Leftrightarrow m \geq \max _{(0 ;+\infty)} g(x) \text { với } g(x)=-3 x^{2}-\frac{3}{4 x^{8}} . \end{array}\)
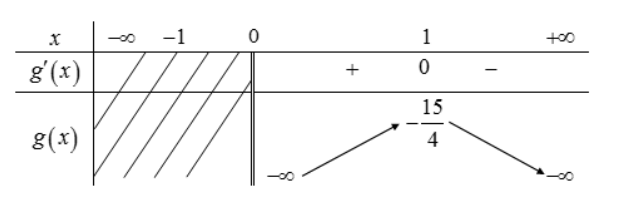
\(\text { Xét } g(x)=-3 x^{2}-\frac{3}{4 x^{8}} \text { trên }(0 ;+\infty), \text { ta có } g^{\prime}(x)=-6 x+\frac{6}{x^{9}} ; g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=1 \\ x=-1 \notin(0 ;+\infty) \end{array}\right. \text { . }\)
Bảng biến thiên:
Suy ra \(m \geq-\frac{15}{4}\)