Cho hàm số \(f(x)=m x^{4}+2 x^{2}-1 \text { với } m\) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2020;2020) sao cho hàm số đã cho đồng biến trên khoảng \(\left(0 ; \frac{1}{2}\right) ?\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
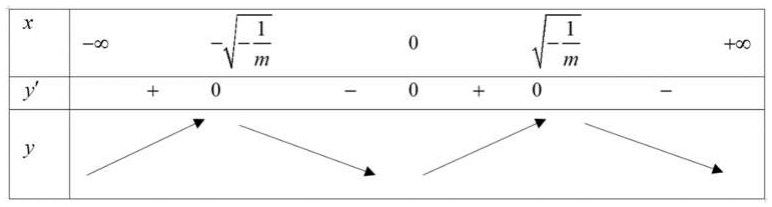
Báo sai\(\begin{array}{l} y^{\prime}=4 m x^{3}+4 x=4 x\left(m x^{2}+1\right) \text { . }\\ m \geq 0: y^{\prime}=4 x\left(m x^{2}+1\right) \geq 0 \Leftrightarrow x \geq 0 \Rightarrow \text { Hàm số đồng biến trên }(0 ;+\infty) \Rightarrow m \geq 0 \text { thỏa mãn. }\\ m<0: y^{\prime}=0 \Leftrightarrow\left[\begin{array} { l } { x = 0 } \\ { x ^ { 2 } = - \frac { 1 } { m } } \end{array} \Leftrightarrow \left[\begin{array}{l} x=0 \\ x=\pm \sqrt{-\frac{1}{m}} \end{array}\right.\right. \end{array}\)
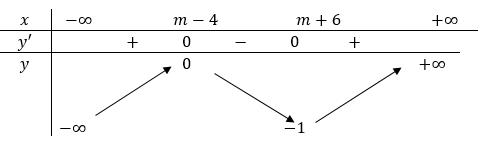
Bảng biến thiên
\(\text { Dựa vào BBT, hàm số đồng biến trên khoảng }\left(0 ; \frac{1}{2}\right) \Leftrightarrow \sqrt{-\frac{1}{m}} \geq \frac{1}{2} \Leftrightarrow-\frac{1}{m} \geq \frac{1}{4} \Leftrightarrow m \leq-4 \text { . }\)
\(\text { So với điều kiện } \Rightarrow m \leq-4 \text { . }\)
\(\text { Mặt khác, theo giả thiết }\left\{\begin{array}{l} m \in(-2020 ; 2020) \\ m \in \mathbb{Z} \end{array}\right.\) suy ra có 4036 giá trị nguyên của m thỏa mãn yêu cầu bài toán