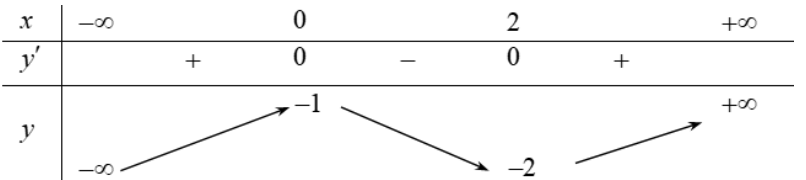
Cho hàm số y=f(x) liên tục trên \(\mathbb{R} \mathrm{V}\) và có bảng biến thiên như sau
Hàm số \(g(x)=f(2-x)-2 \) đồng biến trên
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ bảng biến thiên ta có hàm số y=f(x) có
\(f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=2 \end{array}, f^{\prime}(x)>0 \Leftrightarrow\left[\begin{array}{l} x<1 \\ x>2 \end{array}, f^{\prime}(x)<0 \Leftrightarrow 0<x<2 \text { và } f(0)=-1, f(2)=-2\right.\right.\)
Xét hàm số \(g(x)=f(2-x)-2 \text { ta có } g^{\prime}(x)=-f^{\prime}(2-x) .\) .
Hàm số g(x) đồng biến khi và chỉ khi:
\(\begin{array}{l} g^{\prime}(x)>0 \Leftrightarrow-f^{\prime}(2-x)>0 \Leftrightarrow f^{\prime}(2-x)<0 \Leftrightarrow 0<2-x<2 \Leftrightarrow 0<x<2 . \\ \end{array}\)
Vậy hàm số đồng biến trên (0;2)
.png)











