Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3\sqrt {x - 1} + m\sqrt {x + 1} = 2\sqrt[4]{{{x^2} - 1}}\) có hai nghiệm thực?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐiều kiện : x ≥ 1
\(\begin{array}{l}
PT \Leftrightarrow 3\frac{{\sqrt {x - 1} }}{{\sqrt {x + 1} }} + m = 2\frac{{\sqrt[4]{{{x^2} - 1}}}}{{\sqrt[4]{{{{\left( {x + 1} \right)}^2}}}}}\\
\Leftrightarrow 3\sqrt {\frac{{x - 1}}{{x + 1}}} + m = 2\sqrt[4]{{\frac{{x - 1}}{{x + 1}}}}t = \sqrt[4]{{\frac{{x - 1}}{{x + 1}}}}
\end{array}\)
Với
Thay vào phương trình ta được m = 2t- 3t2 = f(t)
Ta c ó đạo hàm f’(t) = 2-6t ta có: f’(t) = 0 khi t = 1/3
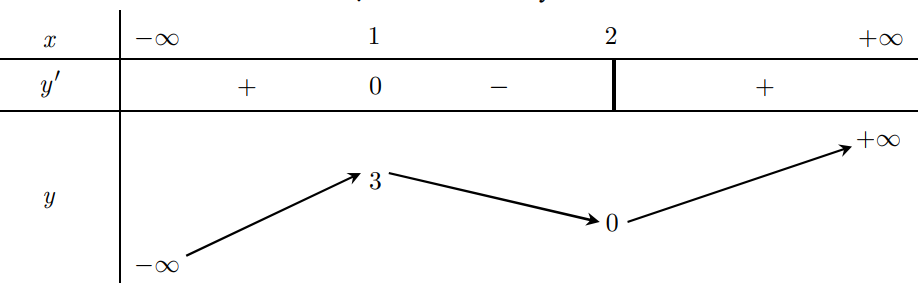
Bảng biến thiên:
Từ bảng biến thiên ta có để phương trình có hai nghiệm khi \(0\le m < \frac{1}{3}\).
ADMICRO
YOMEDIA
ZUNIA9