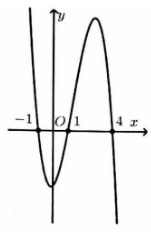
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực \(\mathbb{R}\). Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi hàm số \(y=f(x^2)\) nghịch biến trong khoảng nào sau đây?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị hàm số y=f'(x):
\(\begin{array}{l} y' = f'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l} x > 4\\ - 1 < x < 1 \end{array} \right.\\ y' = f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} x < - 1\\ 1 < x < 4 \end{array} \right. \end{array}\)
Xét hàm số \(y = f({x^2}) \Rightarrow y' = 2x.f'({x^2})\)
Hàm số nghịch biến suy ra:
\(y' < 0 \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ f'({x^2}) < 0 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ f'\left( {{x^2}} \right) > 0 \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ \left[ \begin{array}{l} - 1 < {x^2} < 1\\ {x^2} > 4 \end{array} \right. \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ \left[ \begin{array}{l} {x^2} < - 1\\ 1 < {x^2} < 4 \end{array} \right. \end{array} \right. \end{array} \right.\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l} \left[ \begin{array}{l} 0 < x < 1\\ x > 2 \end{array} \right.\\ - 2 < x < - 1 \end{array} \right. \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Leftrightarrow x \in \left( { - 2; - 2} \right) \cup \left( {0;1} \right) \cup \left( {2; + \infty } \right)\)
chọn câu D
Câu hỏi liên quan
-
Cho hàm số \(y=f(x)=x^{3}+m x^{2}+2 x+3 \text { . }\)Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R là?
-
Tìm tham số m để hàm số \(y=\frac{1}{3}(m-1) x^{3}+m x^{2}+(3 m-2) x\) là hàm đồng biến trên tập xác định của nó?
-
Tổng của các giá trị nguyên của tham số m để hàm số \(y=\frac{x+2}{x+5 m}\) đồng biến trên khoảng \((-\infty ;-10)\)là?
-
Cho hàm số \(y=\frac{m \cot x+8}{2 \cot x+m}\)( m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảg \(\left(\frac{\pi}{4} ; \frac{\pi}{2}\right) ?\)
-
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) là đúng?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=-\frac{1}{3} x^{3}-m x^{2}+(2 m-3) x-m+2\) luôn nghịch biến trên \(\mathbb{R}\) ?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=x^{4}-2(m-1) x^{2}+m-2\) đồng biến trên khoảng (1; 3) ?
-
Tìm m để hàm số \(y = {x^3} – 3m{x^2} + 3\left( {2m – 1} \right) + 1\) đồng biến trên \(\mathbb{R}\).
-
Hàm số \(y = \frac{{5 – 2x}}{{x + 3}}\) nghịch biến trên
-
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - x\) nghịch biến trên khoảng nào sau đây?
-
Cho hàm số \(y = \sqrt {2{x^2} + 1} \). Mệnh đề nào dưới đây đúng?
-
Cho hàm số f x có bảng biến thiên như sau
Hàm số \(y=(f(x))^{3}-3(f(x))^{2}\) nghịch biến trên khoảng nào dưới đây?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{mx + 2m + 1}}{{x - m}}\) nghịch biến trên khoảng (0;+∞).
-
Hàm số \(y=\frac{x+2}{x-1}\)nghịch biến trên các khoảng:
-
Hỏi hàm số \(y = - 2{x^3} + 3{x^2} + 2\) đồng biến trên khoảng nào?
-
Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=\frac{x^{2}-(m+1)+2 m-1}{x-m}\) tăng trên từng khoảng xác định của nó?
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x^{2}-2 x, \forall x \in \mathbb{R}\) . Hàm số \(y=-2f(x)\) đồng biến trên khoảng
-
Số giá trị nguyên thuộc [-5;5] của tham số m sao cho hàm số \(y=\frac{\sin x-m}{\sin x+m}\) nghịch biến trên
khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là -
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\frac{m-1}{3} x^{3}+m x^{2}+(3 m-2) x\) đồng biến trên \((-\infty ;+\infty)\)?
