Tất cả các giá trị thực của tham số m sao cho hàm số \(y=-x^{4}+(2 m-3) x^{2}+m\) nghịch biến trên khoảng là \((1 ; 2) \text { là }\left(-\infty ; \frac{p}{q}\right]\) trong đó phân số \(\frac{p}{q}\) tối giản và q > 0 . Hỏi tổng p+ q là
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTXĐ: \(D=\mathbb{R} . \text { Ta có } y^{\prime}=-4 x^{3}+2(2 m-3) x\)
Hàm số nghịch biến trên \((1 ; 2) \Leftrightarrow y^{\prime} \leq 0, \forall x \in(1 ; 2) \Leftrightarrow m \leq x^{2}+\frac{3}{2}=g(x), \forall x \in(1 ; 2)\)
Xét hàm số g(x), \(g^{\prime}(x)=2 x=0 \Leftrightarrow x=0\)
Bảng biến thiên g(x)
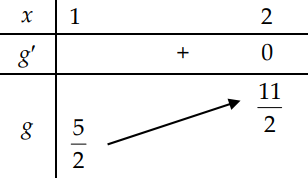
Vậy \(m \leq \min g(x) \Leftrightarrow m \leq \frac{5}{2} . \text { Vậy } p+q=5+2=7\)
ADMICRO
YOMEDIA
ZUNIA9