Tìm tất cả các giá trị của \(m\) để phương trình \({{\log }_{\frac{3}{2}}}\left| x-2 \right|-{{\log }_{\frac{2}{3}}}\left( x+1 \right)=m\) có ba nghiệm phân biệt.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐiều kiện: \(-1<x\ne 2.\)
Phương trình đã cho tương đương với \({{\log }_{\frac{3}{2}}}\left| x-2 \right|+{{\log }_{\frac{3}{2}}}\left( x+1 \right)=m\)
\(\overset{{}}{\longleftrightarrow}{{\log }_{\frac{3}{2}}}\left( \left| x-2 \right|\left( x+1 \right) \right)=m\overset{{}}{\longleftrightarrow}\left| x-2 \right|\left( x+1 \right)={{\left( \frac{3}{2} \right)}^{m}}.\) \(\left( * \right)\)
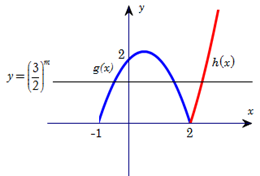
Phương trình \(\left( * \right)\) là phương trình hoành độ giao điểm của đồ thị hàm số \(f\left( x \right)=\left| x-2 \right|\left( x+1 \right)\) và đường thẳng \(y={{\left( \frac{3}{2} \right)}^{m}}\) (cùng phương với trục hoành).
Xét hàm số \(f\left( x \right)=\left| x-2 \right|\left( x+1 \right)\) xác định trên \(\left( -1;2 \right)\cup \left( 2;+\infty \right)\).
Ta có \(f\left( x \right) = \left| {x - 2} \right|\left( {x + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {h\left( x \right) = \left( {x - 2} \right)\left( {x + 1} \right) = {x^2} - x - 2}&{{\rm{khi }}x > 2}\\ {g\left( x \right) = - \left( {x - 2} \right)\left( {x + 1} \right) = - {x^2} + x + 2}&{{\rm{khi }} - 1 < x < 2} \end{array}} \right.\).
Đồ thị
Dựa vào đồ thị, ta thấy để phương trình có ba nghiệm phân biệt khi
\(0 < {\left( {\frac{3}{2}} \right)^m} < \mathop {\max }\limits_{\left( { - 1;2} \right)} g\left( x \right)\).
\( \Leftrightarrow {\left( {\frac{3}{2}} \right)^m} < \frac{9}{4} \Leftrightarrow m < 2\)