Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y = {x^4} - 2m{x^2}\) có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
+ Điều kiện để hàm số có 3 cực trị là m > 0
\(\begin{array}{l}
y' = 4{x^3} - 4mx\\
y' = 0 \Rightarrow \left[ \begin{array}{l}
{x_1} = 0\\
{x_2} = - \sqrt m \\
{x_3} = \sqrt m
\end{array} \right. \Rightarrow \left[ \begin{array}{l}
{y_1} = 0\\
{y_2} = - {m^2}\\
{y_3} = - {m^2}
\end{array} \right.
\end{array}\)
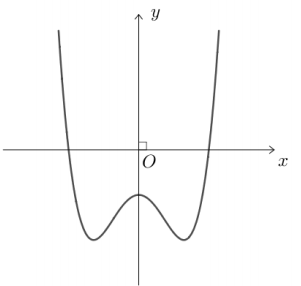
+ Các điểm cực trị tạo thành tam giác cân có đáy bằng \(2\sqrt m \), đường cao bằng m2. (như hình bên )
Ta được \({S_{ABC}} = \frac{1}{2}AC.BD = \sqrt m .{m^2}.\)
+ Để tam giác có diện tích nhỏ hơn 1 thì
Câu hỏi liên quan
-
Số điểm cực đại của hàm số \(f\left( x \right) = - 4{{\rm{x}}^4} - 2{{\rm{x}}^2} + 4\) là
-
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 1} \right)x\) có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.
-
Số cực trị của hàm số \(f\left( x \right) = \frac{1}{4}{{\rm{x}}^4} + \frac{1}{2}{{\rm{x}}^2} + 3\) là
-
Hàm số \(y = {x^4} + 3{x^2} – 4\) có bao nhiêu điểm cực trị?
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
-
Hàm số \(y = \frac{{2x – 5}}{{x + 1}}\) có bao nhiêu điểm cực trị?
-
Số cực trị của hàm số \(f\left( x \right) = {{\rm{x}}^4} + \frac{5}{4}{{\rm{x}}^2} - 12\) là
-
Biết hàm số y = x3 – 3x + 1 có hai điểm cực trị x1; x2 . Tính tổng x12 + x22.
-
Cho hàm số \(y = – {x^4} + 2017{x^2} – 2018\). Số điểm cực trị của đồ thị hàm số là
-
Cho hàm số y=f(x)có bảng biến thiên như sau
Đồ thị hàm số \(y=|f(x)|\) có bao nhiêu điểm cực trị?
-
Điểm cực đại của hàm số \(y=x^{4}-2 x^{2}+2\) là:
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = - 5{{\rm{x}}^4} - 2{{\rm{x}}^2} + 3\) là
-
Số điểm cực đại của hàm số \(f\left( x \right) = {{\rm{x}}^4} + \frac{5}{4}{{\rm{x}}^2} - 12\) là
-
Cho hàm số y=f(x) có \(f'\left( x \right) = {\left( {x + 1} \right)}^{2022}{\left( {x + 2} \right)}.x{\left( {x - 1} \right)^2}\). Điểm cực đại của hàm số là
-
Điểm cực đại của đồ thị hàm số \(y = {x^4} - 2{x^2} + 4\) là:
-
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số \(y=x^{3}-3 x^{2}+4\) là?
-
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=|f(x)| có tất cả bao nhiêu điểm cực trị?
.png)
-
Hàm số nào dưới đây có cực trị?
-
Hàm số y=f(x) có đạo hàm \(f'(x)= ( x -1)( x - 2)...( x - 2019) \,\,\,\forall x\in \mathbb{R} \). Hàm số y=f(x) có tất cả bao nhiêu điểm cực tiểu?
-
Cho đồ thị hàm số y=f(x) xác địn, liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
