Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên \(SA = a\sqrt 3 \)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai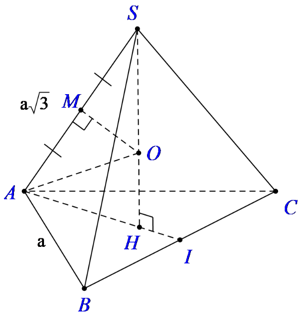
Gọi H là tâm của tam giác đều ABC, ta có SH⊥(ABC) nên SH là trục của tam giác ABC.
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA = OB = OC
Suy ra: O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC. Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có \(\frac{{SO}}{{SA}} = \frac{{SM}}{{SH}}\)
Ta có:
\(\begin{array}{l}
AI = \frac{{a\sqrt 3 }}{2};AH = \frac{2}{3}AI = \frac{{a\sqrt 3 }}{3}\\
SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {3{a^2} - \frac{{3{a^2}}}{9}} = \frac{{2a\sqrt 6 }}{3}\\
\Rightarrow R = SO = \frac{{SM.SA}}{{SH}} = \frac{{S{A^2}}}{{2SH}} = \frac{{3{a^2}}}{{2.\frac{{2a\sqrt 6 }}{3}}} = \frac{{3a\sqrt 6 }}{8}
\end{array}\)
Câu hỏi liên quan
-
Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a. Tam giác ABC vuông tại A có \(B C=2 a \sqrt{3}\). Thể tích của hình trụ ngoại tiếp khối lăng trụ này là:
-
Cho hình nón có đường sinh l, góc giữa đường sinh và mặt phẳng đáy là 30⁰ . Diện tích xung quanh của hình nón này là
-
Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ (T) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của (T) bằng:
-
Thể tích vật thể tròn xoay được giới hạn bởi các đường \(y = \sqrt {1 - {x^2}} ,y = 0,x = 0\) khi quay quanh trục Oy là
-
Một cái cốc hình trụ cao 15cm đựng được 0,5 lít nước. Hỏi bán kính đường tròn đáy đáy của cốc xấp xỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai)?
-
Một hình nón có bán kính đáy là 5a, độ dài đường sinh là 13a thì đường cao h của hình nón là
-
Gọi (r,l,h ) lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón. Chọn mệnh đề đúng:
-
Cho hình trụ có thiết diện qua trục là hình vuông có cạnh bằng (2a ). Thể tích của khối trụ giới hạn bởi hình trụ đã cho bằng:
-
Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền 2a. Thể tích của khối nón bằng
-
Cho hình chóp S.ABC có SA = 8, SA vuông góc với đáy. Tam giác ABC vuông tại A, BC = 7. Tính bán kính của mặt cầu ngoại tiếp khối chóp.
-
Một hình nón có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng \(9\pi \). Tính đường cao h của hình nón.
-
Cho hình chữ nhật ABCD(kể cả miền trong), quay hình chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là:
-
Quay tam giác (ABC ) vuông tại (A ) quanh trục (AB ) ta được:
-
Cho hình trụ có bán kính đáy \(r=\sqrt 3\) và chiều cao h=4 . Diện tích xung quanh của hình trụ bằng.
-
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
-
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = \({a\sqrt 2 }\) và góc giữa A’B và mặt phẳng (ABC) là 60o. Bán kính của mặt cầu ngoại tiếp lăng trụ là:
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
-
Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối lăng trụ đã cho bằng
-
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua trục là một hình vuông. Thể tích khối trụ là:
-
Cắt hình nón bởi một mặt phẳng qua trục thu được thiết diện là một tam giác vuông có diện tích bằng 8. Diện tích xung quanh của hình nón đã cho bằng:
