Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {2;0;0} \right);B\left( {0;3;0} \right);C\left( {0;0; – 4} \right)\). Gọi H là trực tâm tam giác ABC. Viết phương trình tham số của đường thẳng OH.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai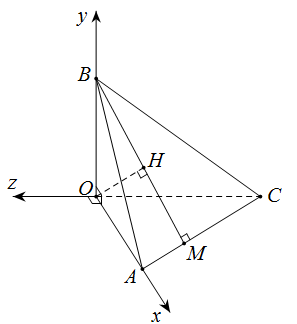
Do \(A \in Ox,B \in Oy,C \in Oz\) nên \(OA,OB,\,OC\) vuông góc từng đôi một.
Ta có \(\left\{ \begin{array}{l}AC \bot OB\\AC \bot BH\end{array} \right. \Rightarrow AC \bot OH\)
Tương tự \(AB \bot OH \Rightarrow OH \bot \left( {ABC} \right)\). Như vậy đường thẳng OH có một véctơ chỉ phương là
\(\overrightarrow u = \left[ {\overrightarrow {AB} ,\,\overrightarrow {BC} } \right] = \left( { – 12; – 8;6} \right) \Rightarrow \overrightarrow u = \left( {6;4; – 3} \right)\) với \(\overrightarrow {AB} = \left( { – 2;3;0} \right);\,\overrightarrow {BC} = \left( {0; – 3; – 4} \right)\)
Phương trình tham số của \(OH:\left\{ \begin{array}{l}x = 6t\\y = 4t\\z = – 3t\end{array} \right.\)











