Xét các hàm số f(x) có đạo hàm\(f^{\prime}(x)=\left(x^{2}-x\right)\left(x^{3}-3 x\right)\) với mọi \(x\in\mathbb{R}\) . Hàm số \(y=|f(1-2019 x)|\)có nhiều nhất bao nhiêu điểm cực trị?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiNhận xét: Số cực trị của hàm số \(y=|f(1-2019 x)|\) bằng tổng số nghiệm của phương trình \(y=f(1-2019 x)\) và số cực trị (không phải là nghiệm phương trình \(y=f(1-2019 x)\) của hàm số \(y=f(1-2019 x)\).
\(\text { Ta có } f^{\prime}(x)=x^{2}(x-1)(x-\sqrt{3})(x+\sqrt{3})\)
\([f(1-2019 x)]^{\prime}=-2019 f^{\prime}(1-2019 x)\)
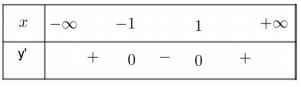
\(\begin{array}{l} {[f(1-2019 x)]^{\prime}=0\\ \Leftrightarrow(1-2019 x)^{2}(1-2019 x-1)(1-2019 x-\sqrt{3})(1-2019 x+\sqrt{3})=0} \\ \Leftrightarrow \quad\left[\begin{array}{l} x=\frac{1}{2019} \\ x=0 \\ x=\frac{1-\sqrt{3}}{2019} \\ x=\frac{1+\sqrt{3}}{2019} \end{array}\right. \end{array}\)
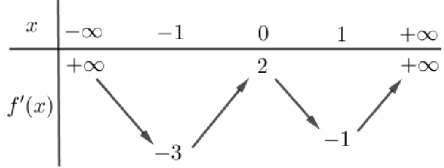
bảng biến thiên của \(y=f(1-2019 x)\)

Do đó phương trình \(f(1-2019 x)=0\)có tối đa 4 nghiệm và hàm số \(f(1-2019 x)=0\) có ba điểm cực trị.
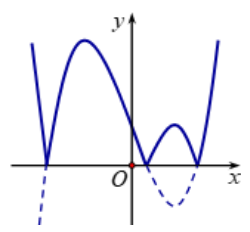
Vậy \(y=|f(1-2019 x)|\) có tối đa 7 cực trị
.png)