Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là sai?
.png)
-
Câu 2:
Giá trị nhỏ nhất của hàm số y = x + e2x trên đoạn [0;2] là
-
Câu 3:
Cho đồ thị hàm số y=ax4+bx2+c đạt cực đại tại A(0;3) và đạt cực tiểu tại B(1;−3). Tính giá trị của biểu thức P = a+3b+2c.
-
Câu 4:
Giá trị lớn nhất của hàm số y=x3 −3x+5 trên đoạn \( \left[ {0;\frac{3}{2}} \right]\)
-
Câu 5:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {0;7} \right]\)
-
Câu 6:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {0;7} \right]\)
-
Câu 7:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 1;3} \right]\)
-
Câu 8:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 1;3} \right]\)
-
Câu 9:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ {2;6} \right]\)
-
Câu 10:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ {2;6} \right]\)
-
Câu 11:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ { - 1;4} \right]\)
-
Câu 12:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ { - 1;4} \right]\)
-
Câu 13:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ { - 5; - 4} \right]\)
-
Câu 14:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ { - 5; - 4} \right]\)
-
Câu 15:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ {0;4} \right]\)
-
Câu 16:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ {0;4} \right]\)
-
Câu 17:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{4x - 7}}{x}\text{ trên đoạn } \left[ { - 5; - 1} \right]\)
-
Câu 18:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{4x - 7}}{x}\text{ trên đoạn } \left[ { - 5; - 1} \right]\)
-
Câu 19:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{4x - 7}}{x}\text{ trên đoạn } \left[ {1;3} \right]\)
-
Câu 20:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{4x - 7}}{x}\text{ trên đoạn } \left[ {1;3} \right]\)
-
Câu 21:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - 2x - 5}}{{x + 3}}\text{ trên đoạn } \left[ {0;5} \right]\)
-
Câu 22:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - 2x - 5}}{{x + 3}}\text{ trên đoạn } \left[ {0;5} \right]\)
-
Câu 23:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - 2x - 5}}{{x + 3}}\text{ trên đoạn } \left[ { - 2;1} \right]\)
-
Câu 24:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - 2x - 5}}{{x + 3}}\text{ trên đoạn } \left[ { - 2;1} \right]\)
-
Câu 25:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x + 3}}{{2x + 5}}\text{ trên đoạn } \left[ { - 5; - 3} \right]\)
-
Câu 26:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - x + 3}}{{2x + 5}}\text{ trên đoạn } \left[ { - 5; - 3} \right]\)
-
Câu 27:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x + 3}}{{2x + 5}}\text{ trên đoạn } \left[ { - 1;2} \right]\)
-
Câu 28:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - x + 3}}{{2x + 5}}\text{ trên đoạn } \left[ { - 1;2} \right]\)
-
Câu 29:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 5; - 3} \right]\)
-
Câu 30:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 5; - 3} \right]\)
-
Câu 31:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {1;5} \right]\)
-
Câu 32:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {1;5} \right]\)
-
Câu 33:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{2x + 9}}{{ - x + 1}}\text{ trên đoạn } \left[ {8;9} \right]\)
-
Câu 34:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{2x + 9}}{{ - x + 1}}\text{ trên đoạn } \left[ {8;9} \right]\)
-
Câu 35:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{2x + 9}}{{ - x + 1}}\text{ trên đoạn } \left[ { - 1;0} \right]\)
-
Câu 36:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{2x + 9}}{{ - x + 1}}\text{ trên đoạn } \left[ { - 1;0} \right]\)
-
Câu 37:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - 1 - 5x}}{x} = \frac{{ - 5x - 1}}{x}\text{ trên đoạn } \left[ { - 5; - 1} \right]\)
-
Câu 38:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - 1 - 5x}}{x} = \frac{{ - 5x - 1}}{x}\text{ trên đoạn } \left[ { - 5; - 1} \right]\)
-
Câu 39:
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - 1 - 5x}}{x} \text{ trên đoạn } \left[ {1;3} \right]\)
-
Câu 40:
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{ - 1 - 5x}}{x} \text{ trên đoạn } \left[ {1;3} \right]\)
-
Câu 41:
Hàm số \(f(x) = \sqrt {3 + x} + \sqrt {5 - x} - 3{x^2} + 6x\)đạt giá trị lớn nhất khi x bằng
-
Câu 42:
Một chất điểm chuyển động theo quy luật s=6t2−t3. Tính thời điểm t (giây) tại đó vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất.
-
Câu 43:
Giá trị lớn nhất của hàm số y=−x2+4x−5 trên đoạn [0;3] bằng
-
Câu 44:
Giá trị nhỏ nhất của hàm số f(x)=x3+3x2−9x−7 trên đoạn [−4;3] bằng:
-
Câu 45:
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
-
Câu 46:
Giá trị lớn nhất của hàm số \( y = \frac{1}{{{x^2} + x + 1}}\) trên khoảng (−∞;+∞):
-
Câu 47:
Giá trị nhỏ nhất của hàm số \( y = \frac{1}{{\sin x + \cos x}}\) trên khoảng \( \left( {0;\frac{\pi }{2}} \right)\)
-
Câu 48:
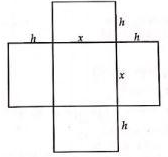
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x(cm) , chiều cao là h (cm) và thể tích là 500cm3. Tìm độ dài cạnh hình vuông sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
-
Câu 49:
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày, \(0≤t≤24\)
-
Câu 50:
Một trang chữ của một quyển sách tham khảo Văn học cần diện tích 384 cm2. Biết rằng trang giấy được canh lề trái là 2cm, lề phải là 2 cm, lề trên 3 cm và lề dưới là 3 cm. Trang sách đạt diện tích nhỏ nhất thì có chiều dài và chiều rộng là: