Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Tìm giá trị nhỏ nhất của hàm số \(y=2 \sin x+\cos 2 x\) trên đoạn \([0 ; \pi]\)
-
Câu 2:
Tìm giá trị lớn nhất của hàm số \(f(x)=x+\sqrt{2} \sin x\) trên đoạn \(\left[-\frac{\pi}{2} ; 0\right]\)
-
Câu 3:
Tìm giá trị nhỏ nhất của hàm số \(y=f(x)=\sqrt{x-2}+\sqrt{8-x}\)
-
Câu 4:
Tìm giá trị lớn nhất của hàm số \(f(x)=\frac{x^{2}-3 x+6}{x-1}\) trên [2;4]
-
Câu 5:
Tìm giá trị lớn nhất và nhỏ nhất của hàm số : \(y=\frac{3 x-1}{x-3}\) trên đoạn [0;2] .
-
Câu 6:
Tìm GTLN của hàm số \(y=2 x^{3}+3 x^{2}-12 x+1\) trên [–1; 5].
-
Câu 7:
Tìm giá trị nhỏ nhất của hàm số \(y=2 \sin ^{2} x+5 \cos ^{2} x-1\)
-
Câu 8:
Tìm giá trị lớn nhất của hàm số \(f(x)=\frac{x^{2}-x+1}{x^{2}+x+1}\)
-
Câu 9:
Tìm giá trị nhỏ nhất của hàm số \(f(x)=\sqrt{x+\frac{1}{x}}\) trên khoảng \((0 ;+\infty)\)?
-
Câu 10:
Tìm giá trị lớn nhất của hàm số \(f(x)=\frac{6-8 x}{x^{2}+1}\) trên khoảng \((-\infty ; 1)\)
-
Câu 11:
Tìm giá trị lớn nhất của hàm số \(f(x)=-\frac{1}{3} x^{6}+\frac{2}{5} x^{5}-\frac{1}{2} x^{2}+x+1\) trên tập xác định.
-
Câu 12:
GTNN của các hàm số sau: \(y=-x^{3}+3 x+1\) trên \([0 ;+\infty)\) là
-
Câu 13:
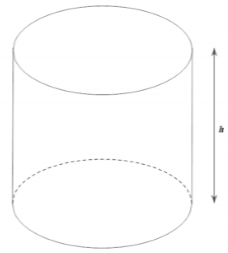
Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn là để ít tốn vật liệu nhất. Gần với giá trị nào nhất
-
Câu 14:
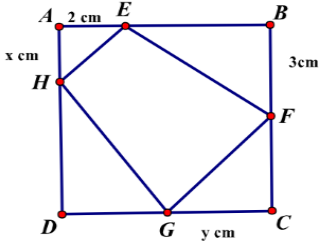
Cho một tấm nhốm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y để dịnh tích hình thang EFGH đạt giá trị nhỏ nhất.
-
Câu 15:
Tìm m để bất phương trình x2-5mx+9 ≥ 0 có nghiệm x ?
-
Câu 16:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{{{x^2}\; + mx\; + 1}}{{x + m}}\) liên tục và đạt giá trị nhỏ nhất trên [0;2] tại một điểm 0 < x0 < 2.
-
Câu 17:
Cho hàm số \(y = \frac{{x + m}}{{x - 1}}\) với tham số m bằng bao nhiêu thì min[2;4] y = 3
-
Câu 18:
Cho hàm số y = x3- 3x+ 1. Tìm tìm tập hợp tất cả giá trị m > 0, để giá trị nhỏ nhất của hàm số trên D = [m+ 1; m+ 2] luôn bé hơn 3 là:
-
Câu 19:
Cho hàm số \(f\left( x \right) = \frac{{2\sqrt x + m}}{{\sqrt {x + 1} }}\) với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
-
Câu 20:
Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\). Với tham số m bằng bao nhiêu thì thỏa mãn \(\mathop {\min }\limits_{\left[ {1;2} \right]} \;y\; + \;\mathop {\max \;y\;}\limits_{\left[ {1;2} \right]} \; = \;\frac{{16}}{3}\;\)?
-
Câu 21:
Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {{x^2} - 2x + m} \right|\) trên đoạn [-1; 2] bằng 5.
-
Câu 22:
Cho hàm số f(x) = \(\frac{{x - {m^2} + m}}{{x + 1}}\) với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.
-
Câu 23:
Cho hàm số y = f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a < b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
-
Câu 24:
Số nguyên nhỏ nhất của tham số để PT \({x^2} + \left( {m + 2} \right)x + 4 = \left( {m - 1} \right)\sqrt {{x^3} + 4x} \) có nghiệm là
-
Câu 25:
Cho hai số thực x, y thỏa mãn x ≥ 0; y ≥ 1 ; x+ y = 3 . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x3+ 2y2+ 3x2+ 4xy- 5x lần lượt bằng:
-
Câu 26:
Tìm m để giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m - 4} \right|\) trên đoạn [-2; 1] đạt giá trị nhỏ nhất. Giá trị của m là
-
Câu 27:
Cho hàm số \(y = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\). Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M ≤ 2m?
-
Câu 28:
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số \(y = \left| {{x^3} - {x^2} + \left( {{m^2} + 1} \right)x - 4m - 7} \right|\) trên đoạn [0; 2], m không vượt quá 15 ?
-
Câu 29:
Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left| {{e^{2x}} - 4{e^x} + m} \right|\) trên [ 0; ln4] bằng 6
-
Câu 30:
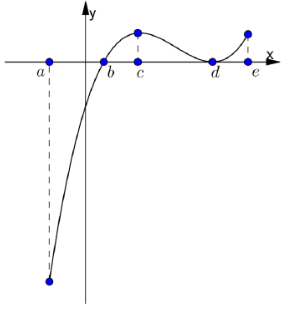
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f(x) trên [ a; e]?
-
Câu 31:
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx2+ (m+ 1) x+ m+1 ≥ 0?
-
Câu 32:
Hàm số y = x8 + (x4 – 1) 2 + 5 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2] lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2 có giá trị bằng:
-
Câu 33:
Hàm số \(y = \sqrt {x + 2} + \sqrt {2 - x} + 2\sqrt {4 - {x^2}} \) đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là:
-
Câu 34:
Hàm số \(y = \sqrt {1 - x} + \sqrt {x + 3} + \sqrt {1 - x} .\sqrt {x + 3} \) có giá trị lớn nhất, giá trị nhỏ nhất là:
-
Câu 35:
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y = 2sin8 x+ cos42x. Khi đó M + m bằng
-
Câu 36:
Giá trị nhỏ nhất của hàm số y= 2sin4x+ cos2x+ 3 bằng
-
Câu 37:
Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sqrt {x - {x^2}} \)?
-
Câu 38:
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = - 3 + \sqrt {4 - {x^2}} \) lần lượt là
-
Câu 39:
Tìm giá trị nhỏ nhất của hàm số \(y = \sqrt {5{x^2} + 4} \) trên đoạn [-3;1].
-
Câu 40:
Giá trị lớn nhất của hàm số y = x3 – 3x + 1 trên [0; 1] là:
-
Câu 41:
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} - 4x}}{{2x + 1}}\) trên đoạn [0;3]
-
Câu 42:
Hàm số y = x3 – 2x2 – 7x + 5 có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3]. Khi đó tổng m + M bằng
-
Câu 43:
Tìm M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [-4;4] là
-
Câu 44:
Tìm giá trị lớn nhất của hàm số \(y = \frac{{3x - 1}}{{x - 3}}\) trên đoạn [0; 2]
-
Câu 45:
Trên đoạn [-1; 1], hàm số \(y = - \frac{4}{3}{x^3} - 2{x^2} - x - 3\)
-
Câu 46:
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn [2 ;4]
-
Câu 47:
Hàm số \(y = \frac{{{x^2} - 3x}}{{x + 1}}\) có giá trị lớn nhất trên đoạn [0;3] là
-
Câu 48:
Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \frac{{x + 3}}{{2x - 1}}\) trên đoạn [1;4]. Tính giá trị biểu thức d = M – m
-
Câu 49:
Cho hàm số có bảng biến thiên ở hình bên. Khẳng định nào sau đây là khẳng định sai?
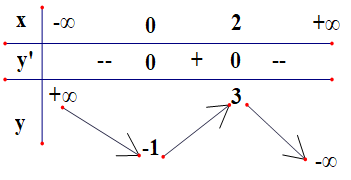
-
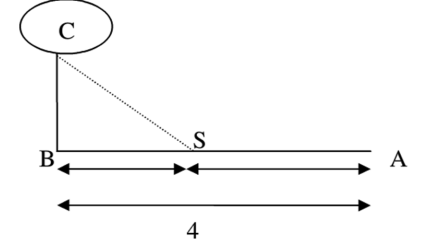
Câu 50:
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C khoảng cách ngắn nhất từ C đến B là 1 km . Khoảng cách từ B đến A là 4 . Mỗi km dây điện đặt dưới nước là mất 5000 USD , còn đặt dưới đất mất 3000 USD . Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi đến C là ít tốn kém nhất?