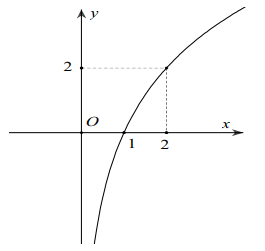Trắc nghiệm Hàm số mũ. Hàm số lôgarit Toán Lớp 12

Câu 1:

Cho hàm số \(y=e x+e^{-x}\) . Nghiệm của phương trình y'=0 ? 

Câu 2:

Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\ln \left(x^{2}-2 m x+4\right)\) có tập xác định D=R ? 

Câu 3:

Tính đạo hàm của hàm số \(y=\left(x^{2}+2 x\right) e^{-x} ?\)

Câu 4:

Tìm tập xác định D của hàm số \(y=\sqrt{\log _{3}(x-2)-3} ?\)

Câu 5:

Tìm tập xác định Dcủa hàm số \(y=\log _{3} \frac{10-x}{x^{2}-3 x+2}\) là?

Câu 6:

Câu 7:

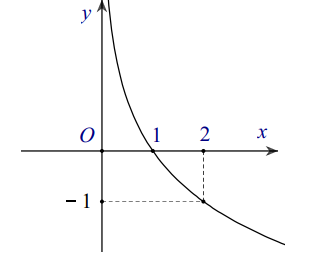
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 

Câu 8:

Cho hàm số \(f(x)=e^{2017 x^{2}}\) . Đạo hàm f'(0) bằng 

Câu 9:

Cho hàm số \(f(x)=\ln \left(x^{4}+1\right)\). Đạo hàm f'(0) bằng:

Câu 10:

Đạo hàm của hàm số \(y=\sin x+\log _{3} x^{3}(x>0)\) là?

Câu 11:

Hàm số \(y=\log _{0,5} x^{2}(x \neq 0)\) có công thức đạo hàm là:

Câu 12:

Đạo hàm của hàm số \(y=\log _{5} x, (x>0)\) là: 

Câu 13:

Đạo hàm của hàm số \(y=4^{2 x}\) là: 

Câu 14:

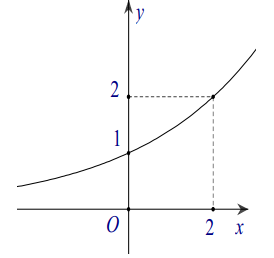
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 

Câu 15:

Hàm số \(y=\log _{x-1} x\) xác định khi và chỉ khi :

Câu 16:

Tập xác định của hàm số \(y=\ln (\ln x)\) là : 

Câu 17:

Tập xác định \(y=\sqrt{-2 x^{2}+5 x-2}+\ln \frac{1}{x^{2}-1}\) là?

Câu 18:

Tập xác định của hàm số \(y=\frac{e^{x}}{e^{x}-1}\) là?

Câu 19:

Tập xác định của hàm số \(y=\frac{1}{\sqrt{2-x}}+\ln (x-1)\) là?

Câu 20:

Tập xác định của hàm số \(y=\log _{2} \frac{x+3}{2-x}\) là?

Câu 21:

Tìm x để hàm số \(y=\log \sqrt{x^{2}+2x-15}\) có nghĩa. 

Câu 22:

Tính giới hạn: \(\mathop {\lim }\limits_{x \to  + \infty } \left( {x{e^{{1 \over x}}} - x} \right)\)

Câu 23:

Tính giới hạn: \(\mathop {\lim }\limits_{x \to 5} \left( {{2^x} - {3^x}} \right)\)

Câu 24:

Tìm giới hạn: \(\mathop {\lim }\limits_{x \to 0} {{{e^{2x}} - {e^{3x}}} \over {5x}}\)

Câu 25:

Tính giới hạn: \(\mathop {\lim }\limits_{x \to 0} {{{e^{3x}} - 1} \over x}\)

Câu 26:

Cho hàm số \(\displaystyle  y = \frac{{\ln x}}{x}\). Chọn khẳng định đúng:

Câu 27:

Đạo hàm của hàm số \(\displaystyle  y = x\left( {\ln x - 1} \right)\) là:

Câu 28:

Hàm số \(\displaystyle  y = \ln \left( {{x^2} - 2mx + 4} \right)\) có tập xác định \(\displaystyle  D = \mathbb{R}\) khi:

Câu 29:

Hàm số \(\displaystyle  y = {x^2}{e^{ - x}}\) tăng trong khoảng:

Câu 30:

Nếu \(\displaystyle  {a^{\frac{{\sqrt 3 }}{3}}} > {a^{\frac{{\sqrt 2 }}{2}}}\) và \(\displaystyle  {\log _b}\frac{3}{4} < {\log _b}\frac{4}{5}\) thì:

Câu 31:

Đạo hàm của hàm số \(\displaystyle y = \frac{{{e^x} - {e^{ - x}}}}{x}\) là:

Câu 32:

Hàm số \(\displaystyle y = {e^x}\sin x\) có đạo hàm là:

Câu 33:

Hàm số \(\displaystyle y = \ln (\cos x)\) có đạo hàm là:

Câu 34:

Hàm số \(\displaystyle y = (3{x^2} - 2){\log _2}x\) có đạo hàm là:

Câu 35:

Hàm số \(\displaystyle y = 3{x^{ - 3}} - {\log _3}x\) có đạo hàm là:

Câu 36:

TXĐ của hàm số \(\displaystyle y = \sqrt {\log (x - 1) + \log (x + 1)} \) là:

Câu 37:

TXĐ của hàm số \(\displaystyle y = \sqrt {\log x + \log (x + 2)} \) là:

Câu 38:

TXĐ của hàm số \(\displaystyle y = {\log _6}\frac{{3x + 2}}{{1 - x}}\) là:

Câu 39:

TXĐ D của hàm số \(\displaystyle y = \frac{2}{{\sqrt {{4^x} - 2} }}\) là:

Câu 40:

Trong các hàm số sau đây, hàm số nào nghịch biến?

Câu 41:

Trong các hàm số sau đây, hàm số nào đồng biến?

Câu 42:

Tìm \(\displaystyle x\), biết \(\displaystyle {\left( {\sqrt 3  - \sqrt 2 } \right)^x} = \sqrt 3  + \sqrt 2 \).

Câu 43:

Tìm \(\displaystyle x\), biết \(\displaystyle {9^x} = \frac {1}{3}\).

Câu 44:

Tìm \(\displaystyle x\), biết \(\displaystyle {\left( {\frac {1}{4}} \right)^x} = 16\).

Câu 45:

Tìm \(\displaystyle x\), biết \(\displaystyle {3^x} = \frac {1}{{81}}\).

Câu 46:

Tìm \(\displaystyle x\), biết \(\displaystyle {2^x} = 64\).

Câu 47:

Với giá trị nào của \(\displaystyle x\) thì đồ thị hàm số \(\displaystyle y = {\left( {\frac {2}{3}} \right)^x}\) nằm phía trên đường thẳng \(\displaystyle y = 1\)?

Câu 48:

Với giá trị nào của \(\displaystyle x\) thì đồ thị hàm số \(\displaystyle y = {4^x}\) nằm phía trên đường thẳng \(\displaystyle y = 1\)?

Câu 49:

Trong các hàm số sau, hàm số nào nghịch biến?

Câu 50:

Trong các hàm số sau, hàm số nào đồng biến?