Cho 2 mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) song song với nhau và cùng cắt khối cầu tâm \(O\) bán kính \(4\sqrt{3}\) thành 2 hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách \(h\) giữa hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai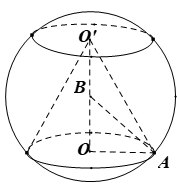
\(d\left( \left( P \right),\left( Q \right) \right)=O{O}'=h\); \(AB=R\).
\(\Delta OAB\) vuông tại \(O\) nên \(OA=\sqrt{A{{B}^{2}}-O{{B}^{2}}}=\sqrt{{{R}^{2}}-\frac{{{h}^{2}}}{4}}.\)
\(\Delta OA{O}'\) vuông tại \(O\) nên \({O}'A=\sqrt{{O}'{{O}^{2}}+O{{A}^{2}}}=\sqrt{{{h}^{2}}+{{R}^{2}}-\frac{{{h}^{2}}}{4}}=\sqrt{{{R}^{2}}+\frac{3{{h}^{2}}}{4}}.\)
Diện tích xung quanh của hình nón: \(S=\pi .OA.{O}'A=\pi .\sqrt{\left( {{R}^{2}}-\frac{{{h}^{2}}}{4} \right).\left( {{R}^{2}}+\frac{3{{h}^{2}}}{4} \right)}\).
Đặt \(x=\frac{{{h}^{2}}}{4},x>0\).
Xét \(f\left( x \right)=\pi .\sqrt{\left( {{R}^{2}}-x \right).\left( {{R}^{2}}+3x \right)}=\pi .\sqrt{{{R}^{4}}+2{{R}^{2}}x-3{{x}^{2}}}\) với \(x\in \left( 0;{{R}^{2}} \right]\).
\({f}'\left( x \right)=\pi .\frac{2{{R}^{2}}-6x}{2\sqrt{\left( {{R}^{2}}-x \right).\left( {{R}^{2}}+3x \right)}}\).
\({f}'\left( x \right)=0\Leftrightarrow 2{{R}^{2}}-6x=0\Leftrightarrow x=\frac{{{R}^{2}}}{3}\).

Diện tích xung quanh của hình nón đạt giá trị lớn nhất khi \(f\left( x \right)\) đạt giá trị lớn nhất trên \(\left( 0;{{R}^{2}} \right]\).
Khi đó \(x=\frac{{{R}^{2}}}{3}\Leftrightarrow \frac{{{h}^{2}}}{4}=\frac{{{R}^{2}}}{3}\Leftrightarrow {{h}^{2}}=\frac{4{{R}^{2}}}{3}\Rightarrow h=\frac{2R\sqrt{3}}{3}=\frac{2\left( 4\sqrt{3} \right)\sqrt{3}}{3}=8\).
Chọn D
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Sương Nguyệt Anh