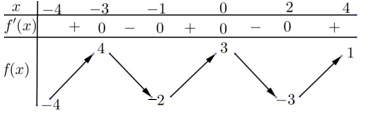
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ -4;\,4 \right]\) và có BBT như hình:

Có tất cả bao nhiêu giá trị thực của tham số \(m\) thuộc đoạn \(\left[ -4;\,4 \right]\) để giá trị lớn nhất của hàm số \(g\left( x \right)=\left| f\left( {{x}^{3}}-3x+2 \right)+2f\left( m \right) \right|\) có giá trị lớn nhất trên đoạn \(\left[ -1;1 \right]\) bằng \(5\)?

Câu hỏi liên quan

• Hình bát diện đều thuộc loại khối đa diện nào? 

• Tích tất cả các nghiệm của phương trình \(\log _{3}^{2}x-2{{\log }_{3}}x-7=0\) là?

• Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số sau \(y=\left| 3{{x}^{4}}-m{{x}^{3}}+6{{x}^{2}}+m-3 \right|\) đồng biến trên khoảng \(\left( 0;+\infty  \right)\)?

ZUNIA12

• Mệnh đề nào dưới đây sai? 

• Cho có tháp nước như hình, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m. Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

  

• Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y={f}'\left( x \right)\) là hàm số bậc 3 có đồ thị là đường cong trong hình:

  

  Hàm số \(y=f\left( x \right)\)nghịch biến trên?

• Tập nghiệm của bất phương trình sau \({{2}^{x\,-\,3}}\,>\,8\) là?

• Cho hàm số \(f\left( x \right)\) có BBT như sau:

  

  Giá trị cực đại của hàm số đã cho là?

• Gọi \(M,m\) lần lượt là GTLN, GTNN của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x-1\) trên đoạn\(\left[ 1;5 \right]\). Tính giá trị \(T=2M-m\)?

• TXĐ của hàm số \(y={{\left( 1-x \right)}^{-2}}\) là?

• Tính thể tích của khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\) là?

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình chóp tạo với mặt đáy góc \(60{}^\circ \). Tính thể tích khối cầu ngoại tiếp hình chóp đã cho?

• Cho hàm số \(y={{x}^{3}}-6{{x}^{2}}+9x+m\text{ }\left( C \right)\), với \(m\) là tham số. Giả sử đồ thị \(\left( C \right)\) cắt trục hoành tại 3 điểm phân biệt có hoành độ thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\). Khẳng định nào sau đây đúng?

• Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC?

   

• Hàm số nào bên dưới đây không có cực trị?

• Cho lăng trụ tam giác \(ABC.A'B'C'\) có thể tích bằng \(V\). Khi đó, thể tích khối chóp \(A.AB{{C}^{'}}\) bằng?

• Cho biểu thức \(\sqrt[3]{4\sqrt{2\sqrt[5]{8}}}={{2}^{\frac{m}{n}}}\), trong đó \(\frac{m}{n}\) là phân số tối giản. Gọi \(P={{m}^{2}}+{{n}^{2}}\). Khẳng định nào đúng? 

• Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ -1;2 \right]\) và có đồ thị như hình. Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ -1;2 \right]\). Ta có \(M+2m\) bằng?

  

• Cho đồ thị \(\left( C \right):y=\frac{x+2}{x-1}\). Gọi \(A,\ B,\ C\) là 3 điểm phân biệt thuộc \(\left( C \right)\) sao cho trực tâm \(H\) của tam giác \(ABC\) thuộc đường thẳng \(\Delta :y=-3x+10\). Độ dài đoạn thẳng \(OH\) bằng?

• Cho hàm số \(y=\frac{x+2}{x-1}\). Xét các mệnh đề sau đây:

  1) Hàm số đã cho đồng biến trên \(\left( 1;+\infty  \right).\)

  2) Hàm số đã cho nghịch biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)

  3) Hàm số đã cho không có điểm cực trị.

  4) Hàm số đã cho nghịch biến trên các khoảng \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty  \right).\)

  Số các mệnh đề đúng là?