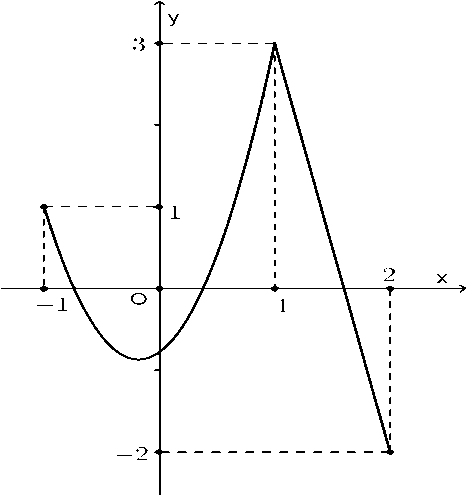
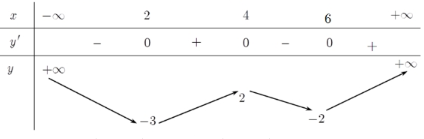
Cho hàm số \(y=f\left( 2-x \right)\) có BBT như sau:
Tổng các giá trị nguyên của tham số \(m\) để phương trình \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\) có đúng 8 nghiệm thực phân biệt thuộc khoảng \(\left( 0;+\infty \right)\)?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số \(g\left( x \right)=f\left( {{x}^{2}}-4x \right)\).
Có \(g'\left( x \right)=\left( 2x-4 \right)f'\left( {{x}^{2}}-4x \right)\). Cho
\(\begin{array}{l}
g'\left( x \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
f'\left( {{x^2} - 4x} \right) = 0\,\,\,\,\left( 1 \right)
\end{array} \right.
\end{array}\).
Ta có:
\(\begin{array}{l}
f'\left( {{x^2} - 4x} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} - 4x = - 4\\
{x^2} - 4x = - 2\\
{x^2} - 4x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
x = 2 \pm \sqrt 2 \\
\left[ \begin{array}{l}
x = 0\\
x = 4
\end{array} \right.
\end{array} \right.
\end{array}\)
Bảng biến thiên
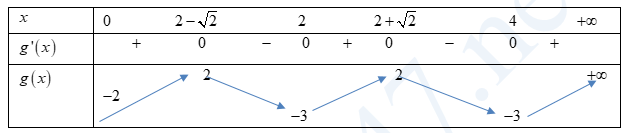
Lại có: \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\)\(\Leftrightarrow 3{{g}^{2}}\left( x \right)-\left( m+2 \right)g\left( x \right)+m-1=0\,\,\left( 2 \right)\).
Ta có: \(\Delta ={{\left( m+2 \right)}^{2}}-4.3.\left( m-1 \right)0={{m}^{2}}-8m+16={{\left( m-4 \right)}^{2}}>0,\forall m\ne 4\).
Dựa vào bảng biến thiên ta thấy phương trình \(g\left( x \right)=h\left( m \right)\) có tối đa là 5 nghiệm phân biệt
Do đó, để phương trình \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\) có đúng 8 nghiệm phân biệt thì
TH1. \(\left\{ \begin{array}{l}
g\left( x \right) = 2\\
- 2 < g\left( x \right) < 2
\end{array} \right.\).
Thế \(g\left( x \right)=2\) vào phương trình (2) ta được \(m=7\). Khi \(m=7\), phương trình (2) có hai nghiệm
\(\left[ \begin{array}{l}
g\left( x \right) = 2\\
g\left( x \right) = 1
\end{array} \right.\) thỏa yêu cầu.
TH2. \(\left\{ \begin{array}{l}
- 3 < g\left( x \right) < - 2\\
- 2 < g\left( x \right) < 2
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
- 3 < \frac{{m + 2 - \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < - 2\\
- 2 < \frac{{m + 2 + \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < 2
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
- 3 < \frac{{m + 2 - \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < - 2\\
- 2 < \frac{{m + 2 + \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < 2
\end{array} \right.\)
Với \(m\ge 4\), ta có:
\(\Leftrightarrow \left\{ \begin{array}{l} - 18 < 6 < - 12\\ - 12 < 2m - 2 < 12 \end{array} \right.\)(vô lí).
Với \(m < 4\), ta có:
\(\Leftrightarrow \left\{ \begin{array}{l} - 18 < 2m - 2 < - 12\\ - 12 < 6 < 12 \end{array} \right. \)\( \Leftrightarrow - 8 < m < - 5\).
Vậy có tổng các giá trị nguyên của tham số \(m\) thỏa yêu cầu đề bài là \(7+\left( -7 \right)+\left( -6 \right)=-6\).
Chọn B
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Sương Nguyệt Anh
Câu hỏi liên quan
-
Cho phương trình sau \(\left( 4\log _{2}^{2}x+{{\log }_{2}}x-5 \right)\sqrt{{{7}^{x}}-m}=0\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của để phương trình đã cho có đúng 2 nghiệm phân biệt?
-
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số sau \(y=\ln \left( {{x}^{2}}-2mx+4 \right)\) có tập xác định là \(\mathbb{R}\)?
-
Có tất cả bao nhiêu cặp số nguyên \(\left( x;y \right)\) thỏa mãn \(0\le x\le 4000\) và \(5\left( {{25}^{y}}+2y \right)=x+{{\log }_{5}}{{\left( x+1 \right)}^{5}}-4\)?
-
Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y={f}'\left( x \right)\) là hàm số bậc 3 có đồ thị là đường cong trong hình:
Hàm số \(y=f\left( x \right)\)nghịch biến trên?
-
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số sau \(y=\left| 3{{x}^{4}}-m{{x}^{3}}+6{{x}^{2}}+m-3 \right|\) đồng biến trên khoảng \(\left( 0;+\infty \right)\)?
-
Tính thể tích của khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\) là?
-
Gọi \(M,m\) lần lượt là GTLN, GTNN của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x-1\) trên đoạn\(\left[ 1;5 \right]\). Tính giá trị \(T=2M-m\)?
-
Gọi \(l,h,r\) lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh \({{S}_{xq}}\) của hình nón là?
-
Cho ĐTHS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình:
Số nghiệm của phương trình \(\left| 2f\left( x \right)-3 \right|=1\) là?
-
Tổng số đường tiệm cận đứng và ngang của ĐTHS \(y=\frac{\sqrt{1-{{x}^{2}}}}{{{x}^{2}}+2x}\) là?
-
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\) cạnh bên \(SA=y\,\,\left( y>0 \right).\) và vuông góc với mp đáy \(\left( ABCD \right)\). Trên cạnh \(AD\) lấy điểm \(M\) và đặt \(AM=x\,(0 < x < a).\) Tính thể tích lớn nhất \({{V}_{\max }}\) của khối chóp \(S.ABCM,\) biết \({{x}^{2}}+{{y}^{2}}={{a}^{2}}\)?
-
Cho biết thể tích \(V\) của khối trụ có chiều cao \(h=4\) cm và bán kính đáy \(r=3\) cm bằng?
-
Cho CSN \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=2\) và công bội \(q=-3\). Giá trị của \({{u}_{2}}\) bằng?
-
Mệnh đề nào dưới đây sai?
-
Tập nghiệm của bất phương trình sau \({{2}^{x\,-\,3}}\,>\,8\) là?
-
Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC?
-
Có tất cả bao nhiêu số nguyên dương của tham số m để hàm số sau \(y=\frac{\cos x+1}{10\cos x+m}\) đồng biến trên khoảng \(\left( 0;\frac{\pi }{2} \right)\cdot \)?
-
Cho hàm số \(y=f\left( x \right)\) xác định trên tập \(D\). Số \(M\) được gọi là GTLN của hàm số \(y=f\left( x \right)\) trên \(D\) nếu?
-
Với các số \(a,\ b>0\) thỏa mãn \({{a}^{2}}+{{b}^{2}}=7ab\), giá trị biểu thức \({{\log }_{3}}\left( a+b \right)\) bằng?
-
Cho có tháp nước như hình, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m. Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?
