Cho hai số thục dương x, y thỏa mãn \(\log _{2} x+x(x+y)=\log _{2}(6-y)+6 x\). Giá trị nhỏ nhất của biểu thức \(T=x^{3}+3 y\) là:
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐKXĐ: \(\left\{\begin{array}{l} x>0 \\ 6-y>0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x>0 \\ y<6 \end{array}\right.\right.\)
Ta có
\(\begin{aligned} & \log _{2} x+x(x+y)=\log _{2}(6-y)+6 x \\ \Leftrightarrow & \log _{2} x+x^{2}+x y=\log _{2}(6-y)+6 x \\ \Leftrightarrow & \log _{2} x+x^{2}=\log _{2}(6-y)+6 x-x y \\ \Leftrightarrow & \log _{2} x+x^{2}=\log _{2}(6-y)+x(6-y) \\ \Leftrightarrow & 2 \log _{2} x+x^{2}=\log _{2}(6-y)+\log _{2} x+x(6-y) \\ \Leftrightarrow & \log _{2} x^{2}+x^{2}=\log _{2}[x(6-y)]+x(6-y) \end{aligned}\)
Xét hàm đặc trưng \(f(t)=\log _{2} t+t(t>0) \text { ta có } f^{\prime}(t)=\frac{1}{t \ln 2}+1>0 \forall t>0\)
\(\Rightarrow\) hàm số đồng biến trên \((0 ;+\infty)\)
Do đó từ \(f\left(x^{2}\right)=f(x(6-y)) \Leftrightarrow x^{2}=x(6-y) \Leftrightarrow x=6-y(\text { Do } x>0) \Leftrightarrow y=6-x\)
Khi đó ta có \(T=x^{3}+3 y=x^{3}+3(6-x)=x^{3}-3 x+18 \text { với } x>0\)
Ta có \(T^{\prime}=3 x^{2}-3=0 \Leftrightarrow x=\pm 1\)
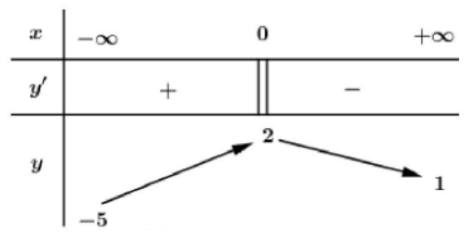
BBT:
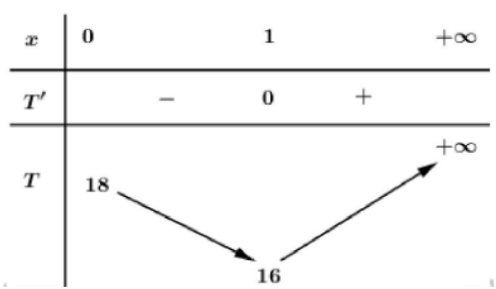
Dựa bào bảng biến thiên ta có \(T_{\min }=T(1)=16\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình