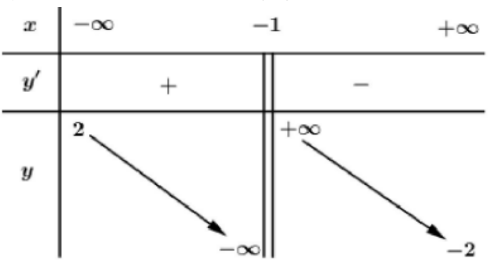
Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \backslash\{-1\},\) có bång biên thiên nhur sau:

Höi đồ thị hàm số \(y=\frac{1}{f(x)}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

Câu hỏi liên quan

• Số phức \(z=a+b i \quad(a, b \in \mathbb{R})\)thòa mãn \(2 z+1=\bar{z},\,\, có \,\,a+b\) bằng:

• Điều kiện cần và đủ đề hàm số \(y=a x^{4}+b x^{2}+c\) có hai điểm cực đại và một điểm cực tiểu là:

• Tính \( \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}\)

ZUNIA12

• Tìm họ nguyên hàm của hàm số \(f(x)=\sin 3 x\)

• Cho hình lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại A . Cạnh BC=2a và \(\widehat{ A B C}=60^{\circ}\) .Biết tứ giác \(B C C^{\prime} B^{\prime}\) là hinh thoi có  \(\widehat{ B^{\prime} B C}\) nhon. Măt phăng \(\left(B C C^{\prime} B^{\prime}\right)\) vuông góc vói (A B C) và măt phẳng \(\left(A B B^{\prime} A^{\prime}\right)\) tạo với (A B C) góc \(45^{\circ} .\) Thể tích khối lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) bằng:

• Số lượng của loại vi khuẩn A trong môt phòng thí nghiệm ước tính theo công thức \(S_{t}=S_{0} \cdot 2^{t}\) trong đó \(S_{0}\) là số lượng vi khuẩn A ban đầu, \(S_{t}\) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lương vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kề từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu  con?

• Hình nón có đường sinh \(l=2 a\) và hợp với đáy góc \(a=60^{\circ}\). Diện tích toàn phần của hình nón bằng:

• Cho hai số thục dương x, y thỏa mãn \(\log _{2} x+x(x+y)=\log _{2}(6-y)+6 x\). Giá trị nhỏ nhất của biểu thức \(T=x^{3}+3 y\) là:

• Trong không gian Oxyz, hai mặt phẳng  \(x-4 y+2 z-7=0\,\, và \,\,2 x-2 y+z+4=0\) chứ hai mặt  của hình lập phương. Thề tích khối lập phương đó là:

• Nếu \(\int\limits_{0}^{m}(2 x-1) d x=2\) thì m có giá trị bằng:

• Tính thề tích V của khối trụ có chu vi đáy là \(2 \pi,\) chiều cao là \(\sqrt{2}\)

• Cho hinh chóp S . A B C D có \(S A \perp(A B C D)\), đáy ABCD là hình chữ nhật có \(A B=a \sqrt{3}, A D=a \sqrt{2}\) Khoảng cách giũra SD và BC bằng:

• Cho hàm số \(f(x)=x^{3}+\left(m^{2}+1\right) x+m^{2}-2\) vói m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.

• Cho f(x) là hàm số liên tục trên tập số thực \(\mathbb{R}\) và thỏa mãn \(f\left(x^{2}+3 x+1\right)=x+2 .\) Tính \(I=\int\limits_{1}^{5} f(x) d x\)

• Trong không gian Oxyz, một vecto chi phương của đường thẳng \(d: \frac{x-1}{1}=\frac{y+2}{-1}=\frac{z}{2}\) là

• Cho hàm số y=f(x) là hàm đa thức bậc ba và có đồ thị như hinh vẽ bên. Khằng định nào sau đây sai?

  

• Biết \(\int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=3 \ln \frac{a}{b}-\frac{5}{6},\) trong đó a, b là các số nguyên dương và \(\frac{a}{b}\) tối gian. Khi dó \(a^{2}-b^{2}\) bằng

• Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \(y=\log _{a} x, y=\log _{b} x, y=\log _{c} x .\)Mệnh đề nào dưới đây đúng?

  

• Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?

  

• Hàm số nào dưới đây không có cực trị: