Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình
-
Câu 1:
Hàm số \(y=\log _{\frac{\pi}{3}}(x-1)\) nghịch biến trên khoảng nào dưới đây?
-
Câu 2:
Tìm họ nguyên hàm của hàm số \(f(x)=\sin 3 x\)
-
Câu 3:
Cho tứ diện ABCD có A B, A C, A D đôi một vuông góc và\(A B=2 a, A C=3 a, A D=4 a\). . Thể tích khối tứ diện là:
-
Câu 4:
Trong không gian Oxyz, một vecto chi phương của đường thẳng \(d: \frac{x-1}{1}=\frac{y+2}{-1}=\frac{z}{2}\) là
-
Câu 5:
Tập nghiệm của bất phưong trình \(\log _{\frac{1}{2}}(x-1) \geq 0\) là
-
Câu 6:
Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?
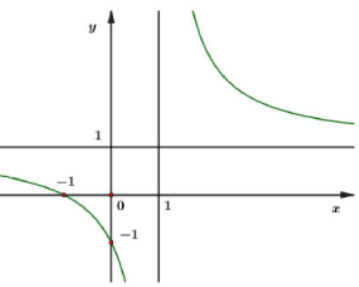
-
Câu 7:
Hàm số nào dưới đây không có cực trị:
-
Câu 8:
Rút gọn biều thúrc \(P=\sqrt[3]{x^{5} \sqrt[4]{x}}\) với x>0
-
Câu 9:
Tim tâp xác định D của hàm số \(y=\left[x^{2}(x+1)\right]^{\frac{1}{2}}\)
-
Câu 10:
Nếu \(\int\limits_{0}^{m}(2 x-1) d x=2\) thì m có giá trị bằng:
-
Câu 11:
Điều kiện cần và đủ đề hàm số \(y=a x^{4}+b x^{2}+c\) có hai điểm cực đại và một điểm cực tiểu là:
-
Câu 12:
Modun của số phức z=2-3i bằng:
-
Câu 13:
Trong không gian Oxyz, cho điểm M (1;-2; 3). Tọa độ điểm A là hình chiếu vuông góc của M trên măt phẳng (O y z) là:
-
Câu 14:
Cho \(\left(u_{n}\right)\) là cấp số nhân \(u_{1}=2, q=3\,. Tính\,\,u_{3}\)
-
Câu 15:
Tập hợp các điềm biều diễn số phúrc z thỏa mãn \(|2 z-1|=1 \)là:
-
Câu 16:
Tìm tất cả các giá trị của m đẻ phương trình \(2^{2 x-1}+m^{2}-m=0\) có nghiệm.
-
Câu 17:
Hình lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông cân tại A có bao nhiêu mặt phẳng đối xứng?
-
Câu 18:
Tính thề tích V của khối trụ có chu vi đáy là \(2 \pi,\) chiều cao là \(\sqrt{2}\)
-
Câu 19:
Số phức \(z=a+b i \quad(a, b \in \mathbb{R})\)thòa mãn \(2 z+1=\bar{z},\,\, có \,\,a+b\) bằng:
-
Câu 20:
Cho hàm số \(f(x)=x^{3}+\left(m^{2}+1\right) x+m^{2}-2\) vói m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
-
Câu 21:
Trong không gian Oxyz, cho điểm A(1 ; 2 ; 3) và B(3 ; 4 ; 7) . Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
-
Câu 22:
Hình nón có đường sinh \(l=2 a\) và hợp với đáy góc \(a=60^{\circ}\). Diện tích toàn phần của hình nón bằng:
-
Câu 23:
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa (các quyển sách cùng đôi một khác nhau). Hỏi có bao nhiêu cách lấy ra 3 quyển sách sao cho ít nhất một quyển sách toán?
-
Câu 24:
Tính \( \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}\)
-
Câu 25:
Cho số thực x thỏa mãn \(2^{x^{2}} \cdot 3^{x+1}=1\). Mệnh đề nào dưới đây đúng?
-
Câu 26:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-x ; y=2 x-2 ; x=0 ; x=3\) được tính bởi công thức
-
Câu 27:
Trong không gian Oxyz, hai mặt phẳng \(x-4 y+2 z-7=0\,\, và \,\,2 x-2 y+z+4=0\) chứ hai mặt của hình lập phương. Thề tích khối lập phương đó là:
-
Câu 28:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
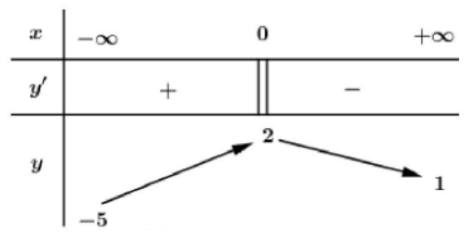
Có bao nhiêu giá trị nguyên của m để phương trình f(x)=m có nghiệm duy nhất?
-
Câu 29:
Trong không gian Oxyz, cho hai mặt phẳng \((\alpha): x+y-z+1=0\,\,và \,\,(\beta):-2 x+m y+2 z-2=0\) Tìm m để \((\alpha)\) song song với \((\beta)\)
-
Câu 30:
Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \(y=\log _{a} x, y=\log _{b} x, y=\log _{c} x .\)Mệnh đề nào dưới đây đúng?
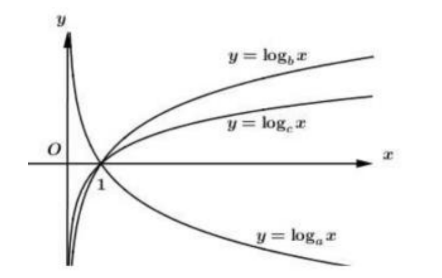
-
Câu 31:
Cho hinh chóp S . A B C D có \(S A \perp(A B C D)\), đáy ABCD là hình chữ nhật có \(A B=a \sqrt{3}, A D=a \sqrt{2}\) Khoảng cách giũra SD và BC bằng:
-
Câu 32:
Xếp ngẫu nhiên 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C vào sáu ghế xếp quanh một bàn tròn (một học sinh ngồi đúng một ghế). Tính xác suất đề học sinh lớp C ngồi giữa 2 học sinh lớp .B
-
Câu 33:
Cho hàm số y=f(x) là hàm đa thức bậc ba và có đồ thị như hinh vẽ bên. Khằng định nào sau đây sai?
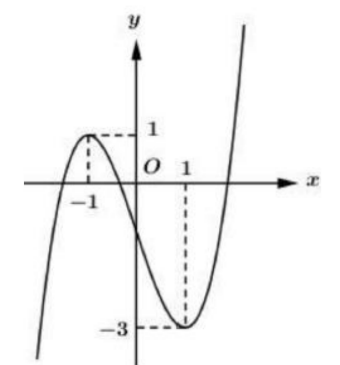
-
Câu 34:
Biết \(\int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=3 \ln \frac{a}{b}-\frac{5}{6},\) trong đó a, b là các số nguyên dương và \(\frac{a}{b}\) tối gian. Khi dó \(a^{2}-b^{2}\) bằng
-
Câu 35:
Cho hàm số y=f(x) thóa mãn\(f(2)=-\frac{4}{19}\,\, và \,\,f^{\prime}(x)=x^{3} f^{2}(x) \forall x \in \mathbb{R} .\) Giá trị của f(1) bằng:
-
Câu 36:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tai A, \(\widehat{ A B C}=30^{\circ}\). Tam giác SAB đều cạnh a và hình chiếu vuông góc cùa S lên mặt phẳng (A B C) là trung điểm của cạnh A B . Thề tích của khối chóp S .ABC là
-
Câu 37:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(2\sqrt{2}\). Canh bên SA vuông góc với mặt phẳng đáy và SA=3 . Mặt phẳng \((\alpha)\) qua A và vuông góc vói SC cắt canh SB, SC, SD lần lươt tai M, N, P . Thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
-
Câu 38:
Cho hàm số y=f(x) thòa mãn f(2)=16 và \(\int\limits_{0}^{2} f(x) d x=4 .\) Tinh \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x\)
-
Câu 39:
Số lượng của loại vi khuẩn A trong môt phòng thí nghiệm ước tính theo công thức \(S_{t}=S_{0} \cdot 2^{t}\) trong đó \(S_{0}\) là số lượng vi khuẩn A ban đầu, \(S_{t}\) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lương vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kề từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
-
Câu 40:
Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \backslash\{-1\},\) có bång biên thiên nhur sau:
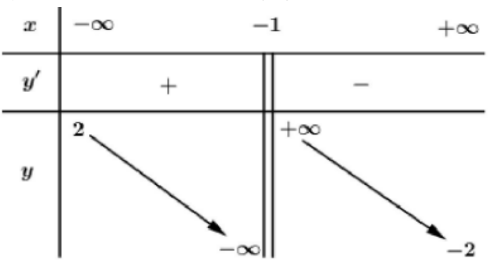
Höi đồ thị hàm số \(y=\frac{1}{f(x)}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
-
Câu 41:
Cho hàm số \(y=(x+2)(x-1)^{2}\) có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với hàm số \(y=|x+2|(x-1)^{2} ?\)
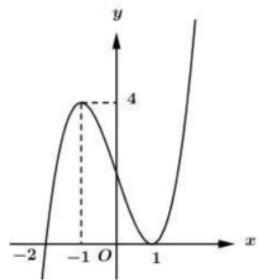
-
Câu 42:
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{x+3}{x-1},\) biết tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân.
-
Câu 43:
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O; cạnh a. Goi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thằng M N và mặt phẳng (A B C D) bằng \(60^{\circ} .\) Tính cos của góc giũa đương thằng MN và măt phẳng (SBD) ?
-
Câu 44:
Cho y=f(x) là hàm đa thức bậc 3 và có đồ thị nhu hình vẽ bên. Hỏi phương trình \(f[f(\cos x)-1]=0\) có bao nhiêu nghiệm thuộc đoan \([0 ; 3 \pi] ?\)
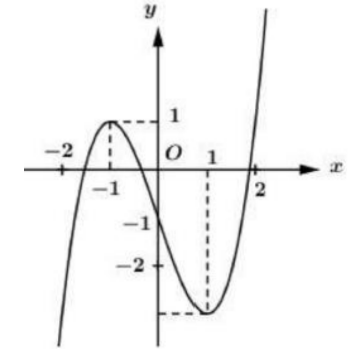
-
Câu 45:
Cho f(x) là hàm số liên tục trên tập số thực \(\mathbb{R}\) và thỏa mãn \(f\left(x^{2}+3 x+1\right)=x+2 .\) Tính \(I=\int\limits_{1}^{5} f(x) d x\)
-
Câu 46:
Có bao nhiêu giá trị nguyên của m hàm số \(y=\left|x^{3}-m x^{2}+12 x+2 m\right|\) luôn đồng biến trên khoảng \((1 ;+\infty) ?\)
-
Câu 47:
Cho phương trình\(\log _{2}^{2} x-(5 m+1) \log _{2} x+4 m^{2}+m=0 .\) Biết phương trình có 2 nghiệm phân biệt \(x_{1}, x_{2}\) thỏa mãn\(x_{1}+x_{2}=165 .\) Giá trị của \(\left|x_{1}-x_{2}\right|\) bằng:
-
Câu 48:
Cho y=f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12 ; 12] để hàm số \(g(x)=|2 f(x-1)+m \mid\) có 5 điểm cực tri?
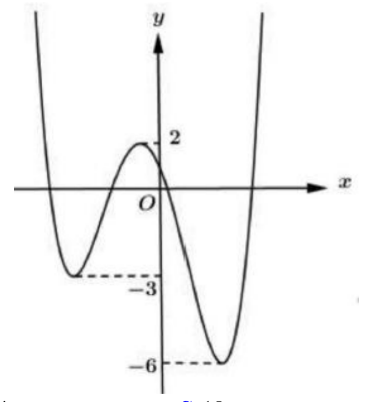
-
Câu 49:
Cho hai số thục dương x, y thỏa mãn \(\log _{2} x+x(x+y)=\log _{2}(6-y)+6 x\). Giá trị nhỏ nhất của biểu thức \(T=x^{3}+3 y\) là:
-
Câu 50:
Cho hình lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại A . Cạnh BC=2a và \(\widehat{ A B C}=60^{\circ}\) .Biết tứ giác \(B C C^{\prime} B^{\prime}\) là hinh thoi có \(\widehat{ B^{\prime} B C}\) nhon. Măt phăng \(\left(B C C^{\prime} B^{\prime}\right)\) vuông góc vói (A B C) và măt phẳng \(\left(A B B^{\prime} A^{\prime}\right)\) tạo với (A B C) góc \(45^{\circ} .\) Thể tích khối lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) bằng:











